Question

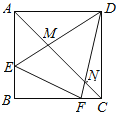
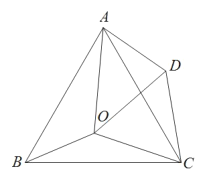
【题目】如图，点是等边内一点，，将绕点按顺时针方向旋转60°得，连接，若，则的度数为__________.

Answer 1

【答案】100°

【解析】

设∠BOC=α，根据旋转前后图形不发生变化，易证△COD是等边三角形，从而利用α分别表示出∠AOD与∠ADO，再根据等腰△AOD的性质求出α．

设∠BOC=α，根据旋转的性质知，△BOC≌△ADC，则OC=DC，∠BOC=∠ADC=α．

又∵△BOC绕点C按顺时针方向旋转60°得到△ADC，

∴∠OCD=60°，

∴△OCD是等边三角形，

∴∠COD=∠CDO=60°，

∵OD=AD，

∴∠AOD=∠DAO．

∵∠AOD=360°-130°-60°-α=170°-α，∠ADO=α-60°，

∴2×（170°-α）+α-60°=180°，

解得α=100°．

故答案是：100°．