题目内容
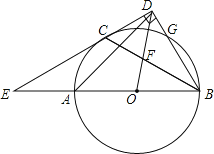
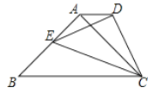
【题目】如图,等腰![]() 为
为![]() 上一点,以
上一点,以![]() 为斜边作等腰
为斜边作等腰![]() ,连接
,连接![]() ,若
,若![]() ,则
,则![]() 的长为________________.
的长为________________.
【答案】![]()
【解析】
由等腰直角三角形的性质得出∠B=∠ACB=45°,BC![]() AB
AB![]() AC
AC![]() ,得出AB=AC=1,由直角三角形的性质得出AC
,得出AB=AC=1,由直角三角形的性质得出AC![]() AE=1,CE=2AE,得出AE
AE=1,CE=2AE,得出AE![]() ,CE
,CE![]() ,BE=AB﹣AE=1
,BE=AB﹣AE=1![]() ,证出∠BCE=∠ACD,
,证出∠BCE=∠ACD,![]() ,得出△BCE∽△ACD,得出比例式,即可得出结果.
,得出△BCE∽△ACD,得出比例式,即可得出结果.
∵等腰Rt△ABC,∠BAC=90°,BC![]() ,
,
∴∠B=∠ACB=45°,BC![]() AB
AB![]() AC
AC![]() ,
,
∴AB=AC=1.
∵∠ACE=30°,
∴AC![]() AE=1,CE=2AE,
AE=1,CE=2AE,
∴AE![]() ,CE
,CE![]() ,
,
∴BE=AB﹣AE=1![]() .
.
∵△CDE是等腰直角三角形,
∴∠DCE=45°,CE![]() CD,
CD,
∴∠BCE=∠ACD,![]() ,
,
∴△BCE∽△ACD,
∴![]() ,
,
∴AD .
.
故答案为:![]() .
.

练习册系列答案
相关题目