题目内容
 如图,已知边长为4的正方形ABCD,E为BC的中点,连接AE、DE,BD、AE交BD于F,连接CF交DE于G,P为DE的中点,连接AP、FP,下列结论:①DE⊥CF;②
如图,已知边长为4的正方形ABCD,E为BC的中点,连接AE、DE,BD、AE交BD于F,连接CF交DE于G,P为DE的中点,连接AP、FP,下列结论:①DE⊥CF;②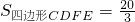 ;③∠EAP=30°;④△FGP为等腰直角三角形.
;③∠EAP=30°;④△FGP为等腰直角三角形.
其中正确结论的个数有
- A.1个
- B.2个
- C.3个
- D.4个
B
分析:根据已知得出首先证明△ABF≌△CBF,得出∠FCB=∠EDC,进而求出∠EGC=90°,再利用△CFM∽△PEQ,得出FM= ,进而求出S△BCD-S△BFE的面积即可得出答案,
,进而求出S△BCD-S△BFE的面积即可得出答案,
再利用等腰直角三角形的知识分析得出答案.
解答: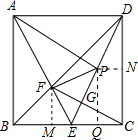 解:作FM⊥BC,
解:作FM⊥BC,
∵∠ABF=∠FBC=45°,
AB=BC,BF=BF,
∴△ABF≌△CBF,
∴∠BAF=∠BCF,
∵边长为4的正方形ABCD,E为BC的中点,
∴AB=CD,BE=CE,∠ABE=∠DCE,
∴△ABE≌△DCE,
∴∠BAE=∠EDC,
∴∠FCB=∠EDC,
∵∠DEC+∠EDC=90°,
∴∠DEC+∠BCF=90°
∴∠EGC=90°,
∴DE⊥CF,故①DE⊥CF正确;
∵△CFM∽△PEQ,
∴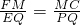 ,
,
∵MC=4-BM,BM=FM,PQ=2,EQ=1,
∴FM= ,
,
∴S△BCD-S△BFE=8- ×2×
×2× =
= ;故②
;故②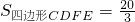 正确;
正确;
∵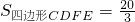 ,
,
∴ CF×DE=
CF×DE= ×2
×2 ×CF=
×CF= ,
,
∴CF= ,
,
∵∠EGC=∠ECD=90°,∠GEC=∠GEC,
∴△CEG∽△DEC,
∴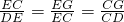 ,
,
∵边长为4的正方形ABCD,E为BC的中点,
∴EC=2,DE=2 ,
,
∴ =
= =
= ,
,
∴EG= ,CG=
,CG= ,
,
∴FG=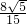 ,PG=
,PG= -
- =
= ,
,
∴FG≠PG,
∴根据已知可得∠FPG≠∠PFG,
∴④△FGP为等腰直角三角形错误.
∵P为DE的中点,
∴PE=DP= ,
,
∴BE=EC=2,AB=CD,
∴△ABE≌△DCE,
∴AE=DE,
∴△AEP为等腰三角形不是等边三角形,
∵P为DE的中点,
∴AP不垂直于DE,
∵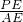 =
= ,
,
∴∠EAP≠30°,故③不正确;
其中正确结论的个数有2个,
故选:B.
点评:此题主要考查了相似三角形的性质与判定以及全等三角形的判定的知识,重点在于对三角形各个性质的理解.主要用到的有中点,中位线的性质.
分析:根据已知得出首先证明△ABF≌△CBF,得出∠FCB=∠EDC,进而求出∠EGC=90°,再利用△CFM∽△PEQ,得出FM=
 ,进而求出S△BCD-S△BFE的面积即可得出答案,
,进而求出S△BCD-S△BFE的面积即可得出答案,再利用等腰直角三角形的知识分析得出答案.
解答:
 解:作FM⊥BC,
解:作FM⊥BC,∵∠ABF=∠FBC=45°,
AB=BC,BF=BF,
∴△ABF≌△CBF,
∴∠BAF=∠BCF,
∵边长为4的正方形ABCD,E为BC的中点,
∴AB=CD,BE=CE,∠ABE=∠DCE,
∴△ABE≌△DCE,
∴∠BAE=∠EDC,
∴∠FCB=∠EDC,
∵∠DEC+∠EDC=90°,
∴∠DEC+∠BCF=90°
∴∠EGC=90°,
∴DE⊥CF,故①DE⊥CF正确;
∵△CFM∽△PEQ,
∴
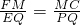 ,
,∵MC=4-BM,BM=FM,PQ=2,EQ=1,
∴FM=
 ,
,∴S△BCD-S△BFE=8-
 ×2×
×2× =
= ;故②
;故②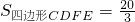 正确;
正确;∵
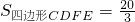 ,
,∴
 CF×DE=
CF×DE= ×2
×2 ×CF=
×CF= ,
,∴CF=
 ,
,∵∠EGC=∠ECD=90°,∠GEC=∠GEC,
∴△CEG∽△DEC,
∴
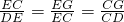 ,
,∵边长为4的正方形ABCD,E为BC的中点,
∴EC=2,DE=2
 ,
,∴
 =
= =
= ,
,∴EG=
 ,CG=
,CG= ,
,∴FG=
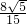 ,PG=
,PG= -
- =
= ,
,∴FG≠PG,
∴根据已知可得∠FPG≠∠PFG,
∴④△FGP为等腰直角三角形错误.
∵P为DE的中点,
∴PE=DP=
 ,
,∴BE=EC=2,AB=CD,
∴△ABE≌△DCE,
∴AE=DE,
∴△AEP为等腰三角形不是等边三角形,
∵P为DE的中点,
∴AP不垂直于DE,
∵
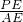 =
= ,
,∴∠EAP≠30°,故③不正确;
其中正确结论的个数有2个,
故选:B.
点评:此题主要考查了相似三角形的性质与判定以及全等三角形的判定的知识,重点在于对三角形各个性质的理解.主要用到的有中点,中位线的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知边长为4的正方形ABCD中,E为AD中点,P为CE中点,F为BP中点,FH⊥BC交BC于H,连接PH,则下列结论正确的是( )
如图,已知边长为4的正方形ABCD中,E为AD中点,P为CE中点,F为BP中点,FH⊥BC交BC于H,连接PH,则下列结论正确的是( )①BE=CE;②sin∠EBP=
| 1 |
| 2 |
| A、①④⑤ | B、①②③ |
| C、①②④ | D、①③④ |
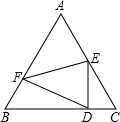 如图,已知边长为5的等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿着EF折叠,使点A落在BC边上的点D的位置,且ED⊥BC,则CE的长是( )
如图,已知边长为5的等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿着EF折叠,使点A落在BC边上的点D的位置,且ED⊥BC,则CE的长是( )A、10
| ||
B、10-5
| ||
C、5
| ||
D、20-10
|
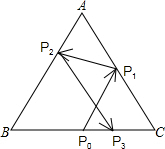 如图,已知边长为2的正三角形ABC中,P0是BC边的中点,一束光线自P0发出射到AC上的点P1后,依次反射到AB、BC上的点P2和P3(反射角等于入射角),且1<BP3<
如图,已知边长为2的正三角形ABC中,P0是BC边的中点,一束光线自P0发出射到AC上的点P1后,依次反射到AB、BC上的点P2和P3(反射角等于入射角),且1<BP3<| 3 |
| 2 |
A、1<P1C<
| ||||
B、
| ||||
C、
| ||||
D、
|
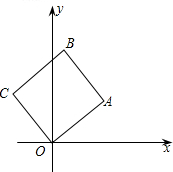 如图,已知边长为l的正方形OABC在直角坐标系中,A、B两点在第一象限内,OA与x轴的夹角为30°,那么点B的坐标是
如图,已知边长为l的正方形OABC在直角坐标系中,A、B两点在第一象限内,OA与x轴的夹角为30°,那么点B的坐标是 用三角函数中正切的两角和公式:tan(α+β)=(tanα+tanβ)÷(1-tanα•tanβ),求出∠CAC′+∠CAA′的度数.( )
用三角函数中正切的两角和公式:tan(α+β)=(tanα+tanβ)÷(1-tanα•tanβ),求出∠CAC′+∠CAA′的度数.( )