题目内容
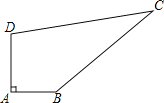
【题目】如图,某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
【答案】7200元.
【解析】
连接BD.在Rt△ABD中,根据勾股定理求得BD=5,在△CBD中,由勾股定理的逆定理判定∠DBC=90°,再由S四边形ABCD=S△BAD+S△DBC求得四边形ABCD的面积,由此即可求得所需费用.
如图,连接BD.

在Rt△ABD中,BD2=AB2+AD2=32+42=52,BD=5;
在△CBD中,CD2=132,BC2=122,而122+52=132,即BC2+BD2=CD2,
∴∠DBC=90°,
S四边形ABCD=S△BAD+S△DBC=![]() AD·AB+
AD·AB+![]() DB·BC=
DB·BC=![]() ×4×3+
×4×3+![]() ×5×12=36,
×5×12=36,
所以需费用36×200=7200(元).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某校在“清明节”前组织七年级全体学生进行了一次“缅怀先烈,牢记历史”知识竞赛,赛后随机抽取了部分学生成绩进行统计,制作如下频数分布表和频数分布直方图,请根据图中提供的信息,解答下列问题:
分数段 | 频数 | 频率 |
| 4 |
|
| 8 | b |
| a |
|
| 10 |
|
| 6 |
|
![]() 表中
表中![]() ______,
______,![]() ______,并补全直方图;
______,并补全直方图;
![]() 若用扇形统计图描述次成绩统计图分别情况,则分数段
若用扇形统计图描述次成绩统计图分别情况,则分数段![]() 对应扇形的圆心角度数是______;
对应扇形的圆心角度数是______;
![]() 若该校七年级共900名学生,请估计该年级分数在
若该校七年级共900名学生,请估计该年级分数在![]() 的学生有多少人?
的学生有多少人?