题目内容
(5分)若P为△ABC所在平面上一点,且∠APB=∠BP C=∠CPA=120°,则点P叫做△ABC的费马点.
【小题1】(1)若点P为锐角△ABC的费马点,且∠ABC=60°,PA=3,PC=4,则PB的值为________;
【小题2】(2)如图,在锐角△ABC外侧作等边△ACB′连结BB′.
求证:BB′过△ABC的费马点P,且BB′=PA+PB+PC.
【小题1】(1)2 .
.
【小题2】(2)在 上取点
上取点 ,使
,使 ,连结
,连结 ,再在
,再在 上截取
上截取 ,连结
,连结 .
.
 ,
, 为正三角形,
为正三角形,
 =
= ,
, 为正三角形,
为正三角形,
 =
= ,
, =
= ,
, ′,
′,
 .
.
 ,
, ,
, 为
为 的费马点,
的费马点, 过
过 的费马点
的费马点 ,且
,且 =
= +
+
解析

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目

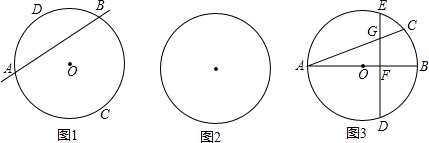 ⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
 ,求S与
,求S与
 ,求S与
,求S与