题目内容
如图,以矩形 的顶点
的顶点 为原点,
为原点, 所在的直线为
所在的直线为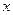 轴,
轴, 所在的直线为
所在的直线为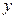 轴,
轴,
建立平面直角坐标系.已知
 为
为 上一动点,点
上一动点,点 以1cm/s的速
以1cm/s的速
度从 点出发向
点出发向 点运动,
点运动, 为
为
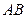 上一动点,点
上一动点,点 以1cm/s的速度从
以1cm/s的速度从 点出发向点
点出发向点 运
运
动.
(1)试写出多边形 的面积
的面积 (
( )与运动时间
)与运动时间 (
( )之间的函数关系式;
)之间的函数关系式;
(2)在(1)的条件下,当多边形 的面积最小时,在坐标轴上是否存在点
的面积最小时,在坐标轴上是否存在点 ,使得
,使得 为等腰三角形?若存在,求出点
为等腰三角形?若存在,求出点 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)在某一时刻将 沿着
沿着 翻折,使得点
翻折,使得点 恰好落在
恰好落在 边的点
边的点 处.求出此时时间t的值.若此时在
处.求出此时时间t的值.若此时在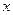 轴上存在一点
轴上存在一点 在
在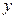 轴上存在一点
轴上存在一点
使得四边形 的周长最小,试求出此时点
的周长最小,试求出此时点 点
点 的坐标.
的坐标.
.(1)∵ ∴
∴




 ………………………………………………………3分
………………………………………………………3分
(2)∵
∴
∴当 时,
时, 有最小值
有最小值
此时:
①当 在
在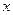 轴上时,设
轴上时,设
此时:


∴当 时,
时,
∴

∴
∵ 与
与 重合 ∴舍去
重合 ∴舍去
当 时,
时,


∴
当 时,
时,


∴

②当 在
在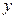 轴上时,设
轴上时,设
则




∴当 时,
时,


∴
当 时,
时, 

 ,∴无解.
,∴无解.
当 时,
时,

∴
∴ (舍
(舍 三点重合)
三点重合)
∴综上共有6个这样的 点
点
使得 为等腰三角形.
为等腰三角形.
即





③设 则
则


∴
过 作
作 于
于
则:
∴
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 的顶点
的顶点 为原点,
为原点, 所在的直线为
所在的直线为 轴,
轴, 所在的直线为
所在的直线为 轴,
轴,
 为
为 点运动,
点运动, 为
为 上一动点,点
上一动点,点 运
运
 的面积
的面积 (
( )与运动时间
)与运动时间 (
( )之间的函数关系式;
)之间的函数关系式; ,使得
,使得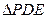 为等腰三角形?若存在,求出点
为等腰三角形?若存在,求出点 沿着
沿着 翻折,使得点
翻折,使得点 边的点
边的点 处.求出此时时间t的值.若此时在
处.求出此时时间t的值.若此时在 在
在
 的周长最小,试求出此时点
的周长最小,试求出此时点 的坐标.
的坐标. 的顶点
的顶点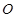 为原点,
为原点, 所在的直线为
所在的直线为 轴,
轴,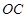 所在的直线为
所在的直线为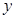 轴,
轴,
 为
为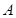 点运动,
点运动,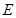 为
为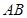 上一动点,点
上一动点,点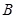 运
运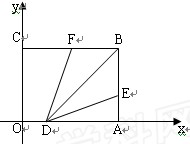
 的面积
的面积 (
(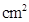 )与运动时间
)与运动时间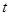 (
(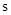 )之间的函数关系式;
)之间的函数关系式;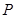 ,使得
,使得 为等腰三角形?若存在,求出点
为等腰三角形?若存在,求出点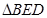 沿着
沿着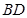 翻折,使得点
翻折,使得点 边的点
边的点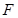 处.求出此时时间t的值.若此时在
处.求出此时时间t的值.若此时在 在
在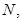
 的周长最小,试求出此时点
的周长最小,试求出此时点 的坐标.
的坐标.