Question

【题目】如图，长方形的边在轴上，边在轴上．把沿折叠得到，与交于点．

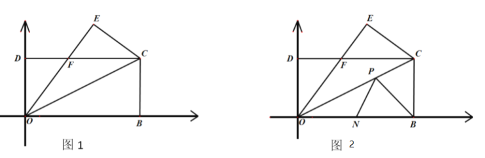
（1）如图1，求证：．

（2）如图1，若，．写出所在直线的解析式．

（3）如图2，在（2）的条件下，是中点，是直线上一动点，是否有最小值，若有请求出最小值，若没有请说明理由．

Answer 1

【答案】（1）见解析；（2）；（3）有最小值，最小值是

【解析】

(1)先依据翻折的性质、矩形的性质证明∠COB=∠COE，∠FCO=∠COB，利用等角对等边即可得到结论；
(2)在Rt△ODF中，依据勾股定理可求得DF的长，从而可得到点F的坐标，然后根据待定系数法即可求得；

(3)由翻折的性质可知点B与点E关于直线OC对称，连接EN交OC于点P，此时PB+PN有最小值，最小值是线段EN，利用勾股定理即可求解．

(1)∵四边形OBCD为矩形，
∴CD∥BO，

∴∠FCO=∠COB，
由翻折的性质可知∠COB=∠COE，
∴∠FCO =∠COE，

∴OF=CF；

(2)∵OF=CF，，．
设，则，
在Rt△ODF中，OD=4，根据勾股定理得，，
∴，
解得：，
∴点F的坐标为(3，4)，
设直线OE的解析式为，
把F(3，4)代入得：，

∴，

∴OE所在直线的解析式为：；

(3)有最小值，理由如下：

由翻折的性质可知点B与点E关于直线OC对称，连接EN交OC于点P，此时PB+PN有最小值，最小值是线段EN，

由翻折的性质可知OE=OB=8，

∵点E在直线上，

∴设点E的坐标为，

在Rt△OEG中，OE=8，OG=，EG=，

∴，即，

解得：，

∴OG=，EG=，

∵是中点，
∴ON=，

∴NG= OG- ON=，

在Rt△NEG中，，，

∴．