题目内容
如图△ABC中，点D、E分别在AC、AB上，AE=3，EB=5，AD=4，DC=2，则
= ．
【答案】分析：先计算AC、AB，然后求
、
的值，发现两个比值相等，而夹角又相等，利用相似三角形的判定可得△AED∽△ACB，再利用相似三角形的面积比等于相似比的平方，可求面积比．
解答：解：∵AE=3，EB=5，AD=4，DC=2，
∴AC=6，AB=8，
∴
=
，
=
，
∴
=
，
又∵∠DAE=∠BAC，
∴△ADE∽△ABC，
∴S△AED：S△ACB=（
）2=
．
点评：本题利用了相似三角形的判定和性质、相似三角形的面积比等于相似比的平方．
、的值，发现两个比值相等，而夹角又相等，利用相似三角形的判定可得△AED∽△ACB，再利用相似三角形的面积比等于相似比的平方，可求面积比．解答：解：∵AE=3，EB=5，AD=4，DC=2，
∴AC=6，AB=8，
∴
=，=，∴
=，又∵∠DAE=∠BAC，
∴△ADE∽△ABC，
∴S△AED：S△ACB=（
）2=．点评：本题利用了相似三角形的判定和性质、相似三角形的面积比等于相似比的平方．
练习册系列答案
相关题目
12、已知：如图△ABC中，点D、E、F分别在三边上，E是AC的中点，AD，BE，CF交于一点G，BD=2DC，S△BGD=8，S△AGE=3，则△ABC的面积是（ ）
16、如图△ABC中，点D在AB上，点E在AC上，且∠BDE+∠C=180°．
如图△ABC中，点D、E分别在AC、AB上，AE=3，EB=5，AD=4，DC=2，则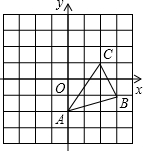
如图△ABC中，点A坐标为（0，-2）．点B坐标为（3，-1）．点C坐标为（2，1）．将图中的△ABC以B为位似中心放大为原来的2倍（即
（2009•裕华区二模）如图△ABC中，点D、E分别在AB、BC边上，DE∥AC，∠B=40°，∠C=70°，那么∠BDE的度数是（ ）