题目内容
已知A(1,-3),C(2,3),则AC绕点O旋转一周扫过的面积为 .
考点:圆的综合题,勾股定理,矩形的判定与性质
专题:计算题
分析:过点A作AB⊥y轴于B,过点C作CD⊥y轴于D,过点O作OH⊥AC于H,过点A作AG⊥DC于G,连接OA、OC,易证四边形ABDG是矩形,则有AG=BD,DG=AB.然后根据勾股定理可求出OC、OA、AC等线段的长,然后运用面积法求出OH的长,由于AC绕点O旋转一周扫过的面积就是AC上离点O最近的点H及最远的点C绕点O旋转一周所围成圆环的面积,因此只要算出该圆环的面积即可解决问题.
解答:解:过点A作AB⊥y轴于B,过点C作CD⊥y轴于D,
过点O作OH⊥AC于H,过点A作AG⊥DC于G,连接OA、OC,如图所示,
则有∠AGD=∠ABD=∠BDG=90°,
∴四边形ABDG是矩形,
∴AG=BD,DG=AB.
∵A(1,-3),C(2,3),
∴AB=1,OB=3,CD=2,OD=3,
∴AG=BD=OB+OD=6,CG=DC-DG=DC-AB=2-1=1.
在Rt△ODC中,OC=
=
,
同理可得:OA=
,AC=
.
∵S△AOC=S梯形ABDC-S△OAB-S△ODC
=
×(1+2)×6-
×1×3-
×2×3=
,
且S△AOC=
AC•OH=
OH,
∴
OH=
,
解得:OH=
.
以点O为圆心,分别以OH、OC为半径画圆,如图所示,
则AC绕点O旋转一周扫过的面积就是图中圆环的面积,
该面积为πOC2-πOH2=13π-
π=
π.
故答案为:
π.
过点O作OH⊥AC于H,过点A作AG⊥DC于G,连接OA、OC,如图所示,
则有∠AGD=∠ABD=∠BDG=90°,
∴四边形ABDG是矩形,
∴AG=BD,DG=AB.

∵A(1,-3),C(2,3),
∴AB=1,OB=3,CD=2,OD=3,
∴AG=BD=OB+OD=6,CG=DC-DG=DC-AB=2-1=1.
在Rt△ODC中,OC=
| OD2+DC2 |
| 13 |
同理可得:OA=
| 10 |
| 37 |
∵S△AOC=S梯形ABDC-S△OAB-S△ODC
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
且S△AOC=
| 1 |
| 2 |
| ||
| 2 |
∴
| ||
| 2 |
| 9 |
| 2 |
解得:OH=
9
| ||
| 37 |
以点O为圆心,分别以OH、OC为半径画圆,如图所示,
则AC绕点O旋转一周扫过的面积就是图中圆环的面积,
该面积为πOC2-πOH2=13π-
| 81 |
| 37 |
| 400 |
| 37 |
故答案为:
| 400 |
| 37 |
点评:本题考查了圆环的面积公式、矩形的判定与性质、勾股定理等知识,在求OH长时用到了面积法,它是求垂线段长常用的一种方法,应掌握它;另外,需要注意的是线段绕某一点旋转一周扫过的面积,并不是线段两个端点绕旋转点旋转一周所围成圆环的面积,而是线段上离旋转点最近的点及最远的点绕旋转点旋转一周所围成圆环的面积.

练习册系列答案
相关题目
 如图,C是△ABE的BE边上一点,F在AE上,D是BC的中点,且AB=AC=CE,下列结论:
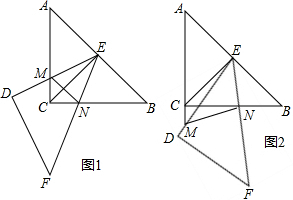
如图,C是△ABE的BE边上一点,F在AE上,D是BC的中点,且AB=AC=CE,下列结论: 如图在△ABC中,∠BAC=90°,AB=AC,CD∥BA,点P是BC上一点,连接AP,过点P作PE⊥AP交CD于E,探究PE与PA的数量关系.
如图在△ABC中,∠BAC=90°,AB=AC,CD∥BA,点P是BC上一点,连接AP,过点P作PE⊥AP交CD于E,探究PE与PA的数量关系.