题目内容
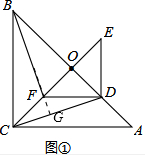
把两个等腰直角三角形△ABC与△DEF如图①摆放,直角顶点D在斜边AB边上,AB、EF的中点均为O,连结BF、CD、CO,显然点C、F、O在同一条直线上.
(1)判断线段BF和CD的数量和位置关系.(直接写出结论不需要证明)
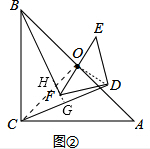
(2)将图①中的Rt△DEF绕点O旋转得到图②,此时(1)中的结论是否成立?证明你的结论;
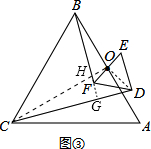
(3)如图③,把题目条件改为△ABC与△DEF都是顶角为2α等腰三角形(即∠ACB=∠EDF=2α),(1)中的数量关系仍然成立吗?如果成立,请说明理由;如不成立,请求出BF与CD之间的数量关系.

(1)判断线段BF和CD的数量和位置关系.(直接写出结论不需要证明)
(2)将图①中的Rt△DEF绕点O旋转得到图②,此时(1)中的结论是否成立?证明你的结论;
(3)如图③,把题目条件改为△ABC与△DEF都是顶角为2α等腰三角形(即∠ACB=∠EDF=2α),(1)中的数量关系仍然成立吗?如果成立,请说明理由;如不成立,请求出BF与CD之间的数量关系.

考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)延长BF与CD交与点G,易证OD=OF,CO=BO,即可证明△BOF≌△COD,可得∠OBF=∠OCG,BF=CD,即可证明∠CFG+∠OCG=90°,即可解题;
(2)连接OD,OF,OF交BF于点H,延长BF交CD于G,易证OD=OF,CO=BO,即可证明△BOF≌△COD,可得∠OBF=∠OCG,BF=CD,即可证明∠CHG+∠OCG=90°,即可解题;
(3)不成立,新结论为BF=CDtanα.理由:连接OD,OF,OF交BF于点H,延长BF交CD于G,易证
=tanα,
=tanα,即可证明△BOF∽△COD,根据相似三角形对应边比例等于相似比即可解题.
(2)连接OD,OF,OF交BF于点H,延长BF交CD于G,易证OD=OF,CO=BO,即可证明△BOF≌△COD,可得∠OBF=∠OCG,BF=CD,即可证明∠CHG+∠OCG=90°,即可解题;
(3)不成立,新结论为BF=CDtanα.理由:连接OD,OF,OF交BF于点H,延长BF交CD于G,易证
| OF |
| OD |
| BO |
| CO |
解答:证明:(1)延长BF与CD交与点G,
∵O是等腰直角△DEF斜边EF中点,
∴EF⊥AB,OD=OF,
∵O是等腰直角△ABC斜边AB中点,
∴CO=BO,
∵在△BOF和△COD中,
∴△BOF≌△COD,(SAS)
∴∠OBF=∠OCG,BF=CD.
∵∠BFO+∠OBF=90°,∠BFO=∠CFG,
∴∠CFG+∠OCG=90°,
∴∠BGC=90°,
∴BF⊥CD;
(2)连接OD,OF,OF交BF于点H,延长BF交CD于G,
∵O是等腰直角△DEF斜边EF中点,
∴OD=OF,∠DOF=90°,
∵O是等腰直角△ABC斜边AB中点,
∴CO=BO,∠BOC=90°,
∴∠BOC+∠COF=∠DOF+∠COF,即∠BOF=∠COD,
∵在△BOF和△COD中,
,
∴△BOF≌△COD,(SAS)
∴∠OBF=∠OCG,BF=CD.
∵∠BHO+∠OBF=90°,∠BHO=∠CHG,
∴∠CHG+∠OCG=90°,
∴∠BGC=90°,
∴BF⊥CD;
(3)不成立,新结论为BF=CDtanα.
理由:连接OD,OC,OC交BF于点H,延长BF交CD于G,
∵O是等腰△DEF底边EF中点,
∴
=tanα,∠DOF=90°,
∵O是等腰△ABC底边AB中点,
∴
=tanα,∠BOC=90°,
∴∠BOC+∠COF=∠DOF+∠COF,即∠BOF=∠COD,
∴△BOF∽△COD,
∴
=
=tanα,
∴BF=CDtanα.

∵O是等腰直角△DEF斜边EF中点,
∴EF⊥AB,OD=OF,
∵O是等腰直角△ABC斜边AB中点,
∴CO=BO,
∵在△BOF和△COD中,
|
∴△BOF≌△COD,(SAS)
∴∠OBF=∠OCG,BF=CD.
∵∠BFO+∠OBF=90°,∠BFO=∠CFG,
∴∠CFG+∠OCG=90°,
∴∠BGC=90°,
∴BF⊥CD;
(2)连接OD,OF,OF交BF于点H,延长BF交CD于G,

∵O是等腰直角△DEF斜边EF中点,
∴OD=OF,∠DOF=90°,
∵O是等腰直角△ABC斜边AB中点,
∴CO=BO,∠BOC=90°,
∴∠BOC+∠COF=∠DOF+∠COF,即∠BOF=∠COD,
∵在△BOF和△COD中,
|
∴△BOF≌△COD,(SAS)
∴∠OBF=∠OCG,BF=CD.
∵∠BHO+∠OBF=90°,∠BHO=∠CHG,
∴∠CHG+∠OCG=90°,
∴∠BGC=90°,
∴BF⊥CD;
(3)不成立,新结论为BF=CDtanα.
理由:连接OD,OC,OC交BF于点H,延长BF交CD于G,

∵O是等腰△DEF底边EF中点,
∴
| OF |
| OD |
∵O是等腰△ABC底边AB中点,
∴
| BO |
| CO |
∴∠BOC+∠COF=∠DOF+∠COF,即∠BOF=∠COD,
∴△BOF∽△COD,
∴
| BF |
| CD |
| BO |
| CO |
∴BF=CDtanα.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了相似三角形对应边比例等于相似比的性质,本题中求证△BOF≌△COD是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
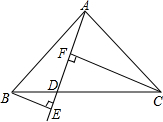 画一个两条直角边相等的直角三角形ABC,并过斜边BC上的一点D画射线AD,分别过B、C画射线AD的垂线BE、CF,垂足为E、F.
画一个两条直角边相等的直角三角形ABC,并过斜边BC上的一点D画射线AD,分别过B、C画射线AD的垂线BE、CF,垂足为E、F. 从图中能数出
从图中能数出 把1~8的数填到图中,使每个四边形中顶点的数字和相等.
把1~8的数填到图中,使每个四边形中顶点的数字和相等. 如图所示,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,将△ABC绕点C逆时针旋转至△A′B′C,使得点A′恰好落在AB上,连接BB′,求BB′的长度.
如图所示,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,将△ABC绕点C逆时针旋转至△A′B′C,使得点A′恰好落在AB上,连接BB′,求BB′的长度.