题目内容
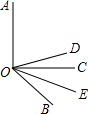 如图所示,已知射线OE平分∠BOC,射线OD平分∠AOB.
如图所示,已知射线OE平分∠BOC,射线OD平分∠AOB.(1)若∠AOC=90°,∠BOC=40°,求∠DOE的度数;
(2)若∠AOC=x°,求∠DOE的度数.
分析:(1)先根据角平分线的定义求得∠BOE=
∠BOC=20°,∠BOD=
∠AOB=
(∠AOC+∠BOC)=65°,再根据∠DOE=∠BOD-∠BOE代入数值求解即可;
(2)解题思路同上.关键是根据角与角之间的数量关系找到∠DOE=∠BOD-∠BOE=
(∠AOC+∠BOC)-
∠BOC=
∠AOC.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)解题思路同上.关键是根据角与角之间的数量关系找到∠DOE=∠BOD-∠BOE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵OE平分∠BOC,
∴∠BOE=
∠BOC=
×40°=20°,
∵OD平分∠AOB,
∴∠BOD=
∠AOB=
(∠AOC+∠BOC)=
×(90°+40°)=65°,
∴∠DOE=∠BOD-∠BOE=65°-20°=45°;
(2)∵OE平分∠BOC,
∴∠BOE=
∠BOC,
又∵OD平分∠AOB,
∴∠BOD=
∠AOB=
(∠AOC+∠BOC),
∴∠DOE=∠BOD-∠BOE=
(∠AOC+∠BOC)-
∠BOC=
∠AOC=
x°.
∴∠BOE=
| 1 |
| 2 |
| 1 |
| 2 |
∵OD平分∠AOB,
∴∠BOD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DOE=∠BOD-∠BOE=65°-20°=45°;
(2)∵OE平分∠BOC,
∴∠BOE=
| 1 |
| 2 |
又∵OD平分∠AOB,
∴∠BOD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DOE=∠BOD-∠BOE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:主要考查了角平分线的定义和角的比较与运算.结合图形找到其中的等量关系:∠DOE=∠BOD-∠BOE=
(∠AOC+∠BOC)-
∠BOC=
∠AOC,是解题的关键.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
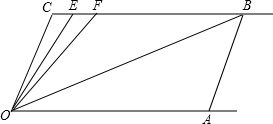
 如图所示,已知射线OC平分∠AOB,∠AOB=60°,∠AOD=50°,则∠COD的度数为
如图所示,已知射线OC平分∠AOB,∠AOB=60°,∠AOD=50°,则∠COD的度数为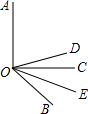 如图所示,已知射线OE平分∠BOC,射线OD平分∠AOB.
如图所示,已知射线OE平分∠BOC,射线OD平分∠AOB.