题目内容
如图,△ABC中,∠B=90°,AB=5,BC=12,将△ABC沿DE折叠,使点C落在AB边上的 处,并且
处,并且 ∥BC,则CD的长是( )
∥BC,则CD的长是( )

A. B.6 C.
B.6 C. D.
D.
A.
【解析】
试题分析:∵∠B=90°,AB=5,BC=12,由勾股定理,得:AC=13.
∵△DEC′与△DEC关于DE成轴对称,∴△DEC′≌△DEC,∴DC′=DC.
∵C′D∥BC,∴△ADC′∽△ACB,∴ ,∴
,∴ ,∴CD=
,∴CD= .故选A.
.故选A.
考点:翻折变换(折叠问题).

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 的正方形
的正方形 中,点
中,点 在
在 延长线上,连接
延长线上,连接 交
交 于点
于点 ,
, (
( ),
), .则在下面函数图象中,大致能反映
.则在下面函数图象中,大致能反映 与
与 之闻函数关系的是( ).
之闻函数关系的是( ).


 ,并写出点A2的坐标.
,并写出点A2的坐标.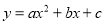 的图象如图所示,则下面四个结论中正确的结论有( )
的图象如图所示,则下面四个结论中正确的结论有( )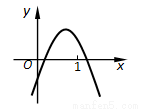
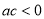 ;②
;②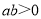 ;③
;③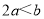 ;④
;④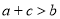 ;⑤
;⑤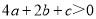 ;⑥
;⑥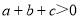 .
.
 ,例如把(3、-2)放入其中,就会得到
,例如把(3、-2)放入其中,就会得到 .现将数对(-2、3)放入其中得到数m,再将数对(m、1)放入其中后,得到的数是____
.现将数对(-2、3)放入其中得到数m,再将数对(m、1)放入其中后,得到的数是____