题目内容
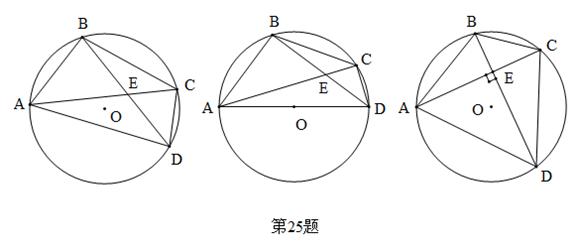
如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)求证:AD平分∠BAC;
(2)若∠BAC = 60°,OA = 2,求阴影部分的面积(结果保留 ).
).

 (1)证明:连接OD.
(1)证明:连接OD.
∵BC是⊙O的切线,D为切点,
∴OD⊥BC.············ 1分
又∵AC⊥BC,
∴OD∥AC,··········· 2分
∴∠ADO=∠CAD.········· 3分
又∵OD=OA,
∴∠ADO=∠OAD,···························· 4分
∴∠CAD=∠OAD,即AD平分∠BA C.····················· 5分
C.····················· 5分
 (2)方法一:连接OE,ED.
(2)方法一:连接OE,ED.
∵∠BAC=60°,OE=OA,
∴△OAE为等边三角形,
∴∠AOE=60°,
∴∠ADE=30°.
又∵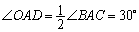 ,
,
∴∠ADE=∠OAD,
∴ED∥AO,············ 6分
∴S△AED=S△OED,
∴阴影部分的面积 = S扇形ODE = 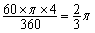 .··············· 9分
.··············· 9分
方法二:同方法一,得ED∥AO,······················ 6分
∴四边形AODE为平行四边形,
∴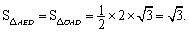 ····················· 7分
····················· 7分
又S扇形ODE-S△OED=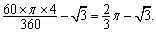 ················· 8分
················· 8分
∴阴影部分的面积 = (S扇形ODE-S△OED) + S△AED =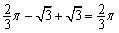 .······ 9分
.······ 9分

练习册系列答案
相关题目

 …………………………………………………………………3分
…………………………………………………………………3分 照上述规律,第2015个单项式是
照上述规律,第2015个单项式是 在△ABC中,BD,CE分别是边AC,AB上的中线,BD与CE相交于点O,则
在△ABC中,BD,CE分别是边AC,AB上的中线,BD与CE相交于点O,则 _________.
_________.
 ;
;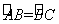 ,AD是⊙O的直径,求证:
,AD是⊙O的直径,求证: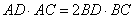 ;
;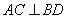 ,点O到AD的距离为2,求BC的长。
,点O到AD的距离为2,求BC的长。