Question

如图，在平面直角坐标系中，已知点A的坐标是（4，0），并且OA=OC=4OB，动点P在过A，B，C三点的抛物线上．

（1）求抛物线的解析式；

（2）是否存在点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；

（3）过动点P作PE垂直于y轴于点E，交直线AC于点D，过点D作y轴的垂线．垂足为F，连接EF，当线段EF的长度最短时，求出点P的坐标．

Answer 1

解：（1）由A（4，0），可知OA=4，

∵OA=OC=4OB，

∴OA=OC=4，OB=1，

∴C（0，4），B（﹣1，0）．

设抛物线的解析式是y=ax²+bx+x，

则，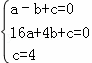

解得：，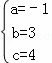

则抛物线的解析式是：y=﹣x²+3x+4；

 

（2）存在．

第一种情况，当以C为直角顶点时，过点C作CP₁⊥AC，交抛物线于点P₁．过点P₁作y轴的垂线，垂足是M．

∵∠ACP₁=90°，

∴∠MCP₁+∠ACO=90°．

∵∠ACO+∠OAC=90°，

∴∠MCP₁=∠OAC．

∵OA=OC，

∴∠MCP₁=∠OAC=45°，

∴∠MCP₁=∠MP₁C，

∴MC=MP₁，

设P（m，﹣m²+3m+4），则m=﹣m²+3m+4﹣4，

解得：m₁=0（舍去），m₂=2．

∴﹣m²+3m+4=6，

即P（2，6）．

第二种情况，当点A为直角顶点时，过A作AP₂，AC交抛物线于点P₂，过点P₂作y轴的垂线，垂足是N，AP交y轴于点F．

∴P₂N∥x轴，

由∠CAO=45°，

∴∠OAP=45°，

∴∠FP₂N=45°，AO=OF．

∴P₂N=NF，

设P₂（n，﹣n²+3n+4），则n=（﹣n²+3n+4）﹣1，

解得：n₁=﹣2，n₂=4（舍去），

∴﹣n²+3n+4=﹣6，

则P₂的坐标是（﹣2，﹣6）．

综上所述，P的坐标是（2，6）或（﹣2，﹣6）；

（3）连接OD，由题意可知，四边形OFDE是矩形，则OD=EF．

根据垂线段最短，可得当OD⊥AC时，OD最短，即EF最短．

由（1）可知，在直角△AOC中，OC=OA=4，

则AC==4，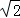

根据等腰三角形的性质，D是AC的中点．

又∵DF∥OC，

∴DF=OC=2，

∴点P的纵坐标是2．

则﹣x²+3x+1=2，

解得：x=，

∴当EF最短时，点P的坐标是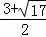：（，0）或（，0）．