题目内容
如图，在矩形ABCD中，AB=10，AD=4，点P是边AB上一点，若△APD与△BPC相似，则满足条件的点P有________个．
3
分析：设AP为x，表示出PB=10-x，然后分AD和PB是对应边，AD和BC是对应边两种情况，利用相似三角形对应边成比例列式求解即可．
解答：
解：设AP为x，
∵AB=10，
∴PB=10-x，
①AD和PB是对应边时，
∵△APD与△BPC相似，
∴
=
，
即
=
，
整理得，x2-10x+16=0，
解得x1=2，x2=8，
②AD和BC是对应边时，
∵△APD与△BPC相似，
∴
=
，
即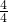
=
，
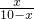解得x=5，
所以，当AP=2、5、8时，△APD与△BPC相似，
满足条件的点P有3个．
故答案为：3．
点评：本题考查了相似三角形的判定，主要利用了相似三角形对应边成比例，难点在于要分情况讨论．
分析：设AP为x，表示出PB=10-x，然后分AD和PB是对应边，AD和BC是对应边两种情况，利用相似三角形对应边成比例列式求解即可．
解答：
解：设AP为x，∵AB=10，
∴PB=10-x，
①AD和PB是对应边时，
∵△APD与△BPC相似，
∴
=，即
=，整理得，x2-10x+16=0，
解得x1=2，x2=8，
②AD和BC是对应边时，
∵△APD与△BPC相似，
∴
=，即
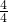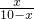=，解得x=5，
所以，当AP=2、5、8时，△APD与△BPC相似，
满足条件的点P有3个．
故答案为：3．
点评：本题考查了相似三角形的判定，主要利用了相似三角形对应边成比例，难点在于要分情况讨论．
练习册系列答案
相关题目
如图，在矩形ABCD中，AB=4cm，BC=8cm，点P从点A出发以1cm/s的速度向点B运动，点Q从点B出发以2cm/s的速度向点C运动，设经过的时间为xs，△PBQ的面积为ycm2，则下列图象能反映y与x之间的函数关系的是（ ）
．
动过程中，Q点停留了1s，图②是P、Q两点在折线AB-BC-CD上相距的路程S（cm）与时间t（s）之间的函数关系图象．
如图，在矩形ABCD中，对角线AC，BD相交于点O，∠AOB=60°，AB=6，则AD=（ ）
DE，EF与AB交于点F，设CE=x，BF=y．