题目内容
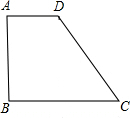
直角梯形ABCD中,AD∥BC,AB⊥BC,AB=10 ,AD=5,BC=15,分别以点C、D为圆心,CB、DA的长为半径作圆,则两圆的位置关系是( )
,AD=5,BC=15,分别以点C、D为圆心,CB、DA的长为半径作圆,则两圆的位置关系是( )A.外切
B.内切
C.相交
D.外离
【答案】分析:首先过点D作DE⊥BC于E,易证得四边形ABED是矩形,然后由勾股定理,求得CD的长,再根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系即可得出两圆位置关系.
解答:解:过点D作DE⊥BC于E,
∵AD∥BC,AB⊥BC,
∴AB∥DE,
∴四边形ABED是矩形,
∴DE=AB=10 ,BE=AD=5,∠DEC=90°,
,BE=AD=5,∠DEC=90°,
∴EC=BA-BE=15-5=10,
∴CD= =20,
=20,
∵AD+BC=20,
∴两圆的位置关系是外切.
故选A.
点评:此题考查了圆与圆的位置关系,梯形的性质,矩形的判定与性质,以及勾股定理的应用等知识.此题难度适中,解题的关键是注意掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系.
解答:解:过点D作DE⊥BC于E,
∵AD∥BC,AB⊥BC,

∴AB∥DE,
∴四边形ABED是矩形,
∴DE=AB=10
 ,BE=AD=5,∠DEC=90°,
,BE=AD=5,∠DEC=90°,∴EC=BA-BE=15-5=10,
∴CD=
 =20,
=20,∵AD+BC=20,
∴两圆的位置关系是外切.
故选A.
点评:此题考查了圆与圆的位置关系,梯形的性质,矩形的判定与性质,以及勾股定理的应用等知识.此题难度适中,解题的关键是注意掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
 在直角梯形ABCD中,底AD=6cm,BC=11cm,腰CD=12cm,则这个直角梯形的周长为
在直角梯形ABCD中,底AD=6cm,BC=11cm,腰CD=12cm,则这个直角梯形的周长为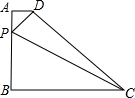 如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=1,BC=8,AB=6,点P在高AB上滑动,当AP长为
如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=1,BC=8,AB=6,点P在高AB上滑动,当AP长为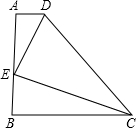 下结论:
下结论: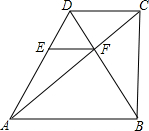 EF∥AB,交AD于点E,CF=4cm.
EF∥AB,交AD于点E,CF=4cm.