题目内容
 如图,点C为线段AB上一点,AC:CB=3:2,D、E两点分别为AC、AB的中点,若线段DE=2cm,则AB的长为( )
如图,点C为线段AB上一点,AC:CB=3:2,D、E两点分别为AC、AB的中点,若线段DE=2cm,则AB的长为( )| A、8cm | B、12cm |
| C、14cm | D、10cm |
考点:两点间的距离
专题:
分析:设AB=x,则AC=
,BC=
,再由线段DE=2cm,根据题目中几何图形,运用方程思想求解.
| 3 |
| 5 |
| 2 |
| 5 |
解答:解:设AB=x,由已知得:
AC=
,BC=
,
∵D、E两点分别为AC、AB的中点,
∴DC=
x,BE=
,
DE=DC-EC=DC-(BE-BC),
即:
x-(
x-
x)=2,
解得:x=10,
则AB的长为10cm.
故选D.
AC=
| 3 |
| 5 |
| 2 |
| 5 |
∵D、E两点分别为AC、AB的中点,
∴DC=
| 3 |
| 10 |
| 1 |
| 2 |
DE=DC-EC=DC-(BE-BC),
即:
| 3 |
| 10 |
| 1 |
| 2 |
| 2 |
| 5 |
解得:x=10,
则AB的长为10cm.
故选D.
点评:本题考查了两点间的距离,利用中点性质转化线段之间的倍分关系是解题的关键,在不同的情况下灵活选用它的不同表示方法,有利于解题的简洁性,同时,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
下列图形中,不属于对称图形的是( )
| A、圆 | B、扇形 |
| C、抛物线 | D、直角边长不相等的直角三角形 |
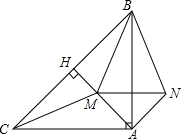 如图,在△ABC中,∠BAC=90°,AB=AC,AH⊥BC于点H,M为线段AH上一点(与A,H不重合)连CM,BM.
如图,在△ABC中,∠BAC=90°,AB=AC,AH⊥BC于点H,M为线段AH上一点(与A,H不重合)连CM,BM. 如图,在方格纸中,我们把每个小正方形的顶点称为格点.己知点A、B、C都在格点上,且每个小正方形的边长都为1.
如图,在方格纸中,我们把每个小正方形的顶点称为格点.己知点A、B、C都在格点上,且每个小正方形的边长都为1.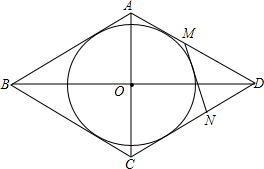 如图,已知菱形ABCD外切于圆O,MN是与AD、CD分别交于M、N的任意一条切线.求证:AM•CN为定值.
如图,已知菱形ABCD外切于圆O,MN是与AD、CD分别交于M、N的任意一条切线.求证:AM•CN为定值.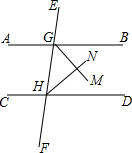 如图,已知GM,HN分别平分∠BGH,∠GHD,GM⊥HN,求证:AB∥CD.
如图,已知GM,HN分别平分∠BGH,∠GHD,GM⊥HN,求证:AB∥CD.