Question

如图，AB是半圆O的直径，且AB＝，矩形CDEF内接于半圆，点C，D在AB上，点E，F在半圆上．

（1）当矩形CDEF相邻两边FC︰CD＝︰2时，求弧AF的度数；

（2）当四边形CDEF是正方形时：

①试求正方形CDEF的边长；

②若点G，M在⊙O上， GH⊥AB于H，MN⊥AB于N，且△GDH和△MHN都是等腰直角三角形，求HN的长．  

 

Answer 1

【答案】

（1）弧AF的度数为60°（2）①4 ②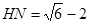

【解析】

试题分析：（1）连结FO，根据圆的对称性，矩形CDEF内接于半圆可得CO＝OD，

∴R t△COF中，FC︰CD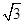＝︰1，∴∠FOC=60°

∴弧AF的度数为60°

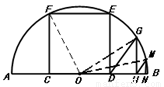
（2）① ∵四边形CDEF是正方形，∴FC=2CO

∵FC²＋CO²=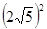，解得CO＝2，∴CF＝4，正方形的边长为4

② 连结OG，OM，∵△GDH和△MHN都是等腰直角三角形，∴DH＝HG，HN＝MN

在R t △OGH中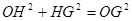，，设DH＝x，则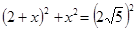

解得x＝2 或x＝－4（舍去）

在R t △OMN中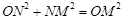，，设HN＝y，

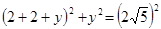∴，解得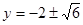（舍去负值）

∴

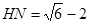
考点：圆的弧度和勾股定理

点评：该题看似复杂，其实所用知识点都是很常见的，求弧的度数主要是看该弧所对圆心角的度数，直角三角形中的边长应多考虑用勾股定理。