题目内容
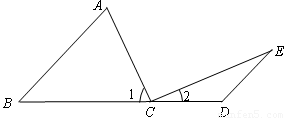
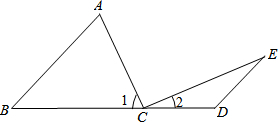 如图:点C在线段BD上,AB∥ED,∠A=∠1,∠E=∠2.
如图:点C在线段BD上,AB∥ED,∠A=∠1,∠E=∠2.(1)若∠B=40°,求∠1、∠2的度数;
(2)判断AC与CE的位置关系,并说明理由.
分析:(1)先根据三角形内角和定理求出∠1的度数,再由平行线的性质求出∠D的度数,由等腰三角形的性质即可得出∠2的度数;
(2)在△ABC中先由三角形内角和定理得出∠1=
(180°-∠B)=90°-
∠B,再根据平行线的性质得出∠B+∠D=180°,在△CDE中,根据∠D+∠E+∠2=180°,∠E=∠2可得出∠2=
∠B,故∠ACE=180°-(∠1+∠2)=180°-(90°-
∠B+
∠B)=90°,由此即可得出结论.
(2)在△ABC中先由三角形内角和定理得出∠1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:(1)解:在△ABC中,
∵∠B+∠A+∠1=180°,∠B=40°,∠A=∠1,
∴∠1=
(180°-∠B)=
(180°-40°)=70°
∵AB∥ED
∴∠B+∠D=180°
∴∠D=180°-40°=140°
在△CDE中,
∵∠D+∠E+∠2=180°,∠E=∠2,
∴∠2=
(180°-∠D)=
(180°-140°)=20°;
(2)AC⊥CE,理由如下:
在△ABC中,
∵∠B+∠A+∠1=180°,∠A=∠1,
∴∠1=
(180°-∠B)=90°-
∠B
∵AB∥ED
∴∠B+∠D=180°
∴∠D=180°-∠B
在△CDE中,
∵∠D+∠E+∠2=180°,∠E=∠2,
∴∠2=
〔180°-∠D〕=
〔180°-(180°-∠B)〕=
∠B,
∴∠ACE=180°-(∠1+∠2)=180°-(90°-
∠B+
∠B)=90°,
∴AC⊥CE
∵∠B+∠A+∠1=180°,∠B=40°,∠A=∠1,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB∥ED
∴∠B+∠D=180°
∴∠D=180°-40°=140°
在△CDE中,
∵∠D+∠E+∠2=180°,∠E=∠2,
∴∠2=
| 1 |
| 2 |
| 1 |
| 2 |
(2)AC⊥CE,理由如下:
在△ABC中,
∵∠B+∠A+∠1=180°,∠A=∠1,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB∥ED
∴∠B+∠D=180°
∴∠D=180°-∠B
在△CDE中,
∵∠D+∠E+∠2=180°,∠E=∠2,
∴∠2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ACE=180°-(∠1+∠2)=180°-(90°-
| 1 |
| 2 |
| 1 |
| 2 |
∴AC⊥CE
点评:本题考查的是平行线的性质,在解答此类问题时往往用到三角形的内角和是180°这一隐含条件.

练习册系列答案
相关题目
 20、如图,点C在线段BD上,△ABD与△ACE都为等边三角形,求∠BDE的度数.
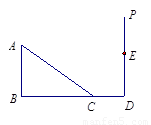
20、如图,点C在线段BD上,△ABD与△ACE都为等边三角形,求∠BDE的度数. 如图,点C在线段BD上,AC⊥BD,CA=CD,点E在线段CA上,且满足DE=AB,连接DE并延长交AB于点F.
如图,点C在线段BD上,AC⊥BD,CA=CD,点E在线段CA上,且满足DE=AB,连接DE并延长交AB于点F.