题目内容
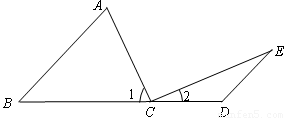
 如图,点C在线段BD上,AC⊥BD,CA=CD,点E在线段CA上,且满足DE=AB,连接DE并延长交AB于点F.
如图,点C在线段BD上,AC⊥BD,CA=CD,点E在线段CA上,且满足DE=AB,连接DE并延长交AB于点F.(1)求证:DE⊥AB;
(2)若已知BC=a,AC=b,AB=c,设EF=x,则△ABD的面积用代数式可表示为;S△ABD=
| 1 | 2 |
分析:(1)首先证明Rt△ABC≌Rt△DCE,得出∠BAC=∠EDC,进而求出∠AFE=180°-(∠BAC+∠AEF)=90°,即可得出答案;
(2)根据S△ABD=S△BCE+S△ACD+S△ABE,S△ABD=
c(c+x)得出a2+b2=c2即可.
(2)根据S△ABD=S△BCE+S△ACD+S△ABE,S△ABD=
| 1 |
| 2 |
解答:(1)证明:在Rt△ABC和Rt△DCE中,
∴Rt△ABC≌Rt△DCE(HL)
∴∠BAC=∠EDC(全等三角形的对应角相等),
∵∠AEF=∠DEC(对顶角相等),∠EDC+∠DEC=90°(直角三角形两锐角互余),
∴∠BAC+∠AEF=∠EDC+∠DEC=90°.
∴∠AFE=180°-(∠BAC+∠AEF)=90°.
∴DE⊥AB.
(2)解:由题意知:
S△ABD=S△BCE+S△ACD+S△ABE=
a2+
b2+
cx,
∵S△ABD=
c(c+x),
∴
a2+
b2+
cx=
c(c+x).
∴a2+b2=c2.
|
∴Rt△ABC≌Rt△DCE(HL)
∴∠BAC=∠EDC(全等三角形的对应角相等),
∵∠AEF=∠DEC(对顶角相等),∠EDC+∠DEC=90°(直角三角形两锐角互余),
∴∠BAC+∠AEF=∠EDC+∠DEC=90°.
∴∠AFE=180°-(∠BAC+∠AEF)=90°.
∴DE⊥AB.
(2)解:由题意知:
S△ABD=S△BCE+S△ACD+S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵S△ABD=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴a2+b2=c2.
点评:此题主要考查了勾股定理的证明和全等三角形的判定与性质,根据图形面积得出S△ABD=S△BCE+S△ACD+S△ABE=
a2+
b2+
cx是解题关键.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 20、如图,点C在线段BD上,△ABD与△ACE都为等边三角形,求∠BDE的度数.
20、如图,点C在线段BD上,△ABD与△ACE都为等边三角形,求∠BDE的度数.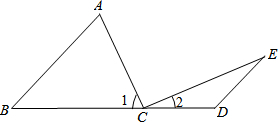 如图:点C在线段BD上,AB∥ED,∠A=∠1,∠E=∠2.
如图:点C在线段BD上,AB∥ED,∠A=∠1,∠E=∠2.