题目内容
【题目】
在平面直角坐标系中的位置如图所示．
（1）作出关于
轴对称的
，并写出各顶点的坐标；
（2）将向右平移6个单位，作出平移后的
并写出各顶点的坐标；
（3）观察和，它们是否关于某直线对称？若是，请用粗线条画出对称轴．
【答案】（1）图见解析；点
，点
，点
；（2）图见解析；点
，点
，点
；（3）是，图见解析
【解析】
（1）先找到A、B、C关于y轴的对称点
，然后连接
、
、
即可，然后根据平面直角坐标系写出A、B、C的坐标，根据关于y轴对称的两点坐标关系：横坐标互为相反数，纵坐标相等即可写出的坐标；
（2）先分别将A、B、C向右平移6个单位，得到
，然后连接
、
、
即可，然后根据平移的坐标规律：横坐标左减右加即可写出的坐标；
（3）根据两个图形成轴对称的定义，画出对称轴即可．
解：（1）先找到A、B、C关于y轴的对称点，然后连接、、，如图所示：
即为所求，
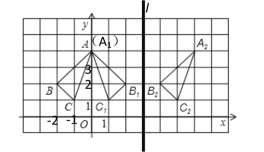
由平面直角坐标系可知：点A（0,4），点B（-2，2），点C（-1，1）
∴点，点，点；
（2）先分别将A、B、C向右平移6个单位，得到，然后连接、、，如图所示：
即为所求，
∵点A（0,4），点B（-2，2），点C（-1，1）
∴点，点，点；
（3）如图所示，和关于直线l对称，所以直线l即为所求．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
