题目内容
【题目】小敏在作⊙O的内接正五边形时,先做了如下几个步骤:
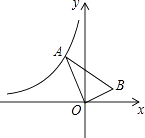
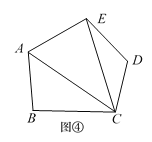
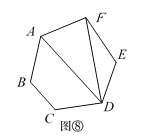
(i)作⊙O的两条互相垂直的直径,再作OA的垂直平分线交OA于点M,如图1;
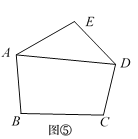
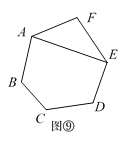
(ii)以M为圆心,BM长为半径作圆弧,交CA于点D,连结BD,如图2.若⊙O的半径为1,则由以上作图得到的关于正五边形边长BD的等式是( )
A.BD2= ![]() OD
OD
B.BD2= ![]() OD
OD
C.BD2= ![]() OD
OD
D.BD2= ![]() OD
OD
【答案】C
【解析】解:如图2,连接BM,
根据题意得:OB=OA=1,AD⊥OB,BM=DM,
∵OA的垂直平分线交OA于点M,
∴OM=AM= ![]() OA=
OA= ![]() ,
,
∴BM= ![]() =
= ![]() ,
,
∴DM= ![]() ,
,
∴OD=DM﹣OM= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴BD2=OD2+OB2= ![]() =
= ![]() =
= ![]() OD.
OD.
故选C.
【考点精析】掌握正多边形和圆是解答本题的根本,需要知道圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等.

练习册系列答案
相关题目