题目内容
6.如图所示,我们以直线上点为端点作一条射线,就得到两个角,这两个角是邻角且互补,像这样的角我们称之为邻补角.例如1与2是邻补角.在第二个图中,∠AOB与∠COB是邻补角,OE,OF分别是∠AOB与∠COB靠近OB的三等分线,求∠EOF的度数.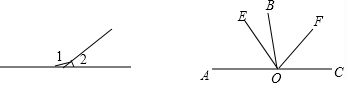
分析 根据三等分线定义可得∠BOE=$\frac{1}{3}$∠AOB,∠BOF=$\frac{1}{3}$∠BOC,再根据邻补角定义可得∠AOB+∠BOC=180°,然后由∠EOF=∠BOE+∠BOF,利用等量代换可得答案.
解答 解:∵∠AOB与∠COB是邻补角,
∴∠AOB+∠BOC=180°,
∵OE,OF分别是∠AOB与∠COB靠近OB的三等分线,
∴∠BOE=$\frac{1}{3}$∠AOB,∠BOF=$\frac{1}{3}$∠BOC,
∴∠EOF=∠BOE+∠BOF=$\frac{1}{3}∠$AOB+$\frac{1}{3}∠$BOC=$\frac{1}{3}$(∠AOB+∠BOC)=$\frac{1}{3}×180°$=60°.
点评 此题主要考查了邻补角和角的三等分线,关键是理清图中角之间的和差关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.如果将抛物线y=(x-1)2+2向下平移1个单位,那么所得的抛物线解析式是( )
| A. | y=(x-1)2+3 | B. | y=(x-1)2+1 | C. | y=(x-2)2+2 | D. | y=x2+2 |
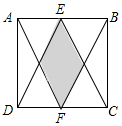 如图,正方形ABCD中,E,F分别为AB,CD的中点,连接DE,BF,CE,AF,正方形ABCD的面积为1,则阴影部分的面积是$\frac{1}{4}$.
如图,正方形ABCD中,E,F分别为AB,CD的中点,连接DE,BF,CE,AF,正方形ABCD的面积为1,则阴影部分的面积是$\frac{1}{4}$.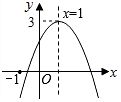 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: