题目内容
当b>0时,一次函数y=ax+b与二次函数y=ax2+bx+c在同一坐标内的图象大致是( )
A、 | B、 | C、 | D、 |
分析:根据b>0说明直线与y轴的交点在y轴的正半轴,当a>0时,抛物线的开口向上,直线是y随x的增大而增大,同时还要看抛物线的对称轴.
解答:解:A:∵b>0,
∴直线与y轴的交点在y轴的正半轴.
所以A错误.
B:根据直线a<0,根据抛物线a>0,
这样是矛盾的.
所以B错误.
C:根据直线与抛物线a>0,
又∵b>0,
∴抛物线的对称轴是:-
<0.
所以C正确.
D:根据直线与抛物线a>0,
∵b>0,∴抛物线的对称轴-
<0,
而图形中抛物线的对称轴是大于0的.
所以D错误.
故选C.
∴直线与y轴的交点在y轴的正半轴.
所以A错误.
B:根据直线a<0,根据抛物线a>0,
这样是矛盾的.
所以B错误.
C:根据直线与抛物线a>0,
又∵b>0,
∴抛物线的对称轴是:-
| b |
| 2a |
所以C正确.
D:根据直线与抛物线a>0,
∵b>0,∴抛物线的对称轴-
| b |
| 2a |
而图形中抛物线的对称轴是大于0的.
所以D错误.
故选C.
点评:本题考查的是二次函数的图象,利用直线与抛物线的图象和性质计算判断,作出正确的选择.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
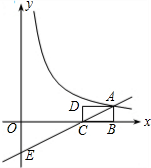 交于点E,反比例函数y=
交于点E,反比例函数y=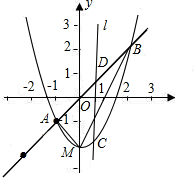 如图,抛物线y=x2-2与直线y=x相交于点A、B.
如图,抛物线y=x2-2与直线y=x相交于点A、B. 如图,已知一次函数y=k1x+b的图象分别与x轴、y轴的正半轴交于A、B两点,且与反比例函数
如图,已知一次函数y=k1x+b的图象分别与x轴、y轴的正半轴交于A、B两点,且与反比例函数 如图,一次函数y=kx+2的图象与反比例函数
如图,一次函数y=kx+2的图象与反比例函数