题目内容
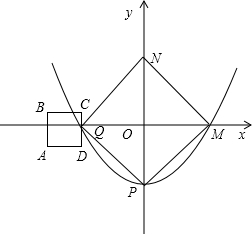 如图,抛物线
如图,抛物线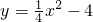 交x轴于点Q、M,交y轴于点P,点P关于x轴的对称点为N.
交x轴于点Q、M,交y轴于点P,点P关于x轴的对称点为N.
(1)求点M、N的坐标,并判断四边形NMPQ的形状;
(2)如图,坐标系中有一正方形ABCD,其中AB=2cm且CD⊥x轴,CD的中点E与Q点重合,正方形ABCD以1cm/s的速度沿射线QM运动,当正方形ABCD完全进入四边形QPMN时立即停止运动.
①当正方形ABCD与四边形NMPQ的交点个数为2时,求两四边形重叠部分的面积y与运动时间t之间的函数关系式,并写出自变量t的取值范围;
②求运动几秒时,重叠部分的面积为正方形ABCD面积的一半.
解:(1)令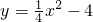 =0,
=0,
解得:x1=4,x2=-4,
∴Q(-4,0),M(4,0),
令x=0,解得y=-4,
∴P(0,-4),
∴点P关于x轴的对称点N的坐标是(0,4),
∴OM=ON=OQ=OP,
又∵NP⊥QM,
∴四边形NMPQ的形状是正方形.
(2)①当0<t≤1时,y=t 2;
当1≤t<2时,y=2t-1;
当t=3时,y=4.
∴y=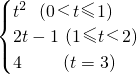 ,
,
②当重叠部分的面积为正方形ABCD面积的一半即S=2时,
即y=2t-1=2,
∴t= ,
,
当2=t2,
t= (不合题意舍去,∵0<t≤1),
(不合题意舍去,∵0<t≤1),
分析:(1)令抛物线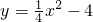 =0,可求出Q,M的横坐标,令x=0,则可求出抛物线和纵轴的交点坐标,利用点关于x轴的对称点的规律可求出N点的坐标,进而可判定四边形NMPQ的形状;
=0,可求出Q,M的横坐标,令x=0,则可求出抛物线和纵轴的交点坐标,利用点关于x轴的对称点的规律可求出N点的坐标,进而可判定四边形NMPQ的形状;
(2)①当正方形ABCD与四边形NMPQ的交点个数为2时,两四边形重叠部分的面积y与运动时间t之间的函数关系式随时间的变化而变化,所以要分类讨论;
②当重叠部分的面积为正方形ABCD面积的一半时,由①中的函数关系式可求出此时的时间t.
点评:本题考查了二次函数与几何知识(正方形)的综合应用,将函数知识与方程、几何知识有机地结合在一起.这类试题一般难度较大.解这类问题关键是善于将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识,并注意挖掘题目中的一些隐含条件.
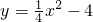 =0,
=0,解得:x1=4,x2=-4,
∴Q(-4,0),M(4,0),
令x=0,解得y=-4,
∴P(0,-4),
∴点P关于x轴的对称点N的坐标是(0,4),
∴OM=ON=OQ=OP,
又∵NP⊥QM,
∴四边形NMPQ的形状是正方形.
(2)①当0<t≤1时,y=t 2;
当1≤t<2时,y=2t-1;
当t=3时,y=4.
∴y=
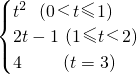 ,
,②当重叠部分的面积为正方形ABCD面积的一半即S=2时,
即y=2t-1=2,
∴t=
 ,
,当2=t2,
t=
 (不合题意舍去,∵0<t≤1),
(不合题意舍去,∵0<t≤1),分析:(1)令抛物线
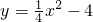 =0,可求出Q,M的横坐标,令x=0,则可求出抛物线和纵轴的交点坐标,利用点关于x轴的对称点的规律可求出N点的坐标,进而可判定四边形NMPQ的形状;
=0,可求出Q,M的横坐标,令x=0,则可求出抛物线和纵轴的交点坐标,利用点关于x轴的对称点的规律可求出N点的坐标,进而可判定四边形NMPQ的形状;(2)①当正方形ABCD与四边形NMPQ的交点个数为2时,两四边形重叠部分的面积y与运动时间t之间的函数关系式随时间的变化而变化,所以要分类讨论;
②当重叠部分的面积为正方形ABCD面积的一半时,由①中的函数关系式可求出此时的时间t.
点评:本题考查了二次函数与几何知识(正方形)的综合应用,将函数知识与方程、几何知识有机地结合在一起.这类试题一般难度较大.解这类问题关键是善于将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识,并注意挖掘题目中的一些隐含条件.

练习册系列答案
相关题目
 如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4).
如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4). 如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,-4).
如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,-4).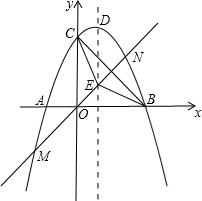 如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4).
如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4).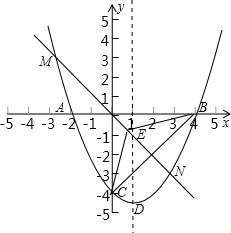 请说明理由.
请说明理由. 交x轴于A、B两点,交y轴于点C,点P是它的顶点,点A的横坐标是-3,点B的横坐标是1。
交x轴于A、B两点,交y轴于点C,点P是它的顶点,点A的横坐标是-3,点B的横坐标是1。 ,
, ,
, )
)