题目内容
平面内有n条直线（n≥2），这n条直线两两相交，最多可以得到a个交点，最少可以得到b个交点，则a+b的值是
- A.n（n-1）
- B.n2-n+1
- C.
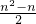
- D.
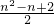
D
分析：分别求出2条直线、3条直线、4条直线、5条直线…的交点个数，找出规律即可解答．
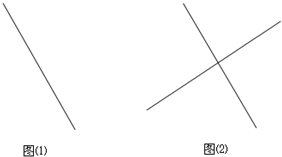
解答：如图：2条直线相交有1个交点；
3条直线相交有1+2个交点；
4条直线相交有1+2+3个交点；
5条直线相交有1+2+3+4个交点；
6条直线相交有1+2+3+4+5个交点；
…
n条直线相交有1+2+3+5+…+（n-1）=
个交点．
所以a=，而b=1，
∴a+b=．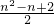
故选D．
点评：本题考查的是直线的交点问题，解答此题的关键是找出规律，需注意的是n条直线相交时最少有一个交点．
分析：分别求出2条直线、3条直线、4条直线、5条直线…的交点个数，找出规律即可解答．
解答：如图：2条直线相交有1个交点；
3条直线相交有1+2个交点；
4条直线相交有1+2+3个交点；
5条直线相交有1+2+3+4个交点；
6条直线相交有1+2+3+4+5个交点；
…
n条直线相交有1+2+3+5+…+（n-1）=
个交点．所以a=
，而b=1，∴a+b=
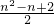．故选D．
点评：本题考查的是直线的交点问题，解答此题的关键是找出规律，需注意的是n条直线相交时最少有一个交点．
练习册系列答案
名校课堂系列答案
相关题目
平面内有n条直线（n≥2），这n条直线两两相交，最多可以得到a个交点，最少可以得到b个交点，则a+b的值是（ ）
| A、n（n-1） | ||
| B、n2-n+1 | ||
C、
| ||
D、
|
