题目内容
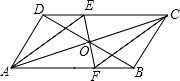
 如图,点O是平行四边形ABCD对角线AC、BD的交点,将直线DB绕点O顺时针方向旋转,交DC、AB于点E、F,若DB=2,AD=1,AB=
如图,点O是平行四边形ABCD对角线AC、BD的交点,将直线DB绕点O顺时针方向旋转,交DC、AB于点E、F,若DB=2,AD=1,AB=| 5 |
(1)求证:当旋转角为90°,四边形AFED是平行四边形;
(2)当旋转角为45°时,判断四边形AECF的形状,并说明理由.
分析:(1)先利用勾股定理的逆定理得出∠ADB=90°,旋转角的定义可得∠DOE=90°,再根据内错角相等,两直线平行可得AD∥EF,根据平行四边形的对边平行可得AF∥DE,然后根据平行四边形的定义即可得证;
(2)先证明四边形AECF的对角线互相垂直,再证明对角线互相平分,然后根据菱形的判定得到四边形AECF是菱形.
(2)先证明四边形AECF的对角线互相垂直,再证明对角线互相平分,然后根据菱形的判定得到四边形AECF是菱形.
解答: (1)证明:∵DB=2,AD=1,AB=
(1)证明:∵DB=2,AD=1,AB=
,
∴DB2+AD2=AB2,
∴∠ADB=90°.
将直线DB绕点O顺时针方向旋转90°时,∠DOE=90°,
∴AD∥EF,
又∵四边形ABCD为平行四边形,
∴AF∥DE,
∴四边形AFED是平行四边形;
 (2)解:∵四边形ABCD是平行四边形,
(2)解:∵四边形ABCD是平行四边形,
∴OD=OB=
DB=1,OA=OC,
∴AD=OD=1,
由(1)知△ABD是直角三角形,且∠ADB=90°,
∴△OAD是等腰直角三角形,
∴∠AOD=45°.
当直线DB绕点O顺时针旋转45°时,即∠DOE=45°,
∴∠AOE=90°,即EF⊥AC.
在△DEO与△BFO中,
,
∴△DEO≌△BFO,
∴OE=OF,
又∵OA=OC,
∴四边形AECF是平行四边形,
∵EF⊥AC,
∴平行四边形AECF是菱形.
 (1)证明:∵DB=2,AD=1,AB=
(1)证明:∵DB=2,AD=1,AB=| 5 |
∴DB2+AD2=AB2,
∴∠ADB=90°.
将直线DB绕点O顺时针方向旋转90°时,∠DOE=90°,
∴AD∥EF,
又∵四边形ABCD为平行四边形,
∴AF∥DE,
∴四边形AFED是平行四边形;
 (2)解:∵四边形ABCD是平行四边形,
(2)解:∵四边形ABCD是平行四边形,∴OD=OB=
| 1 |
| 2 |
∴AD=OD=1,
由(1)知△ABD是直角三角形,且∠ADB=90°,
∴△OAD是等腰直角三角形,
∴∠AOD=45°.
当直线DB绕点O顺时针旋转45°时,即∠DOE=45°,
∴∠AOE=90°,即EF⊥AC.
在△DEO与△BFO中,
|
∴△DEO≌△BFO,
∴OE=OF,
又∵OA=OC,
∴四边形AECF是平行四边形,
∵EF⊥AC,
∴平行四边形AECF是菱形.
点评:此题考查了勾股定理的逆定理,旋转的性质,平行线的判定,平行四边形、全等三角形的判定与性质,菱形的判定,综合性较强,有一定难度.

练习册系列答案
相关题目
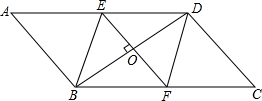 别交于点E、F.
别交于点E、F. 
 如图,在四边形ABCD中,点E、F、G、H分别是各边的中点,则按要求完成下列题目.
如图,在四边形ABCD中,点E、F、G、H分别是各边的中点,则按要求完成下列题目.
