题目内容
计算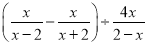
的结果是( )
A. -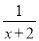
B. 
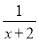C. -1 D. 1
A
【解析】试题解析：原式故答案是A选项
故选A.
练习册系列答案
相关题目
下列推理中，错误的是( )
A. ∵∠A＝∠B＝∠C，∴△ABC是等边三角形
B. ∵AB＝AC，且∠B＝∠C，∴△ABC是等边三角形
C. ∵∠A＝60°，∠B＝60°，∴△ABC是等边三角形
D. ∵AB＝AC，∠B＝60°，∴△ABC是等边三角形
B
【解析】A∵∠A＝∠B＝∠C，∴△ABC是等边三角形，故正确；
B条件重复且条件不足，故不正确；
C∵∠A＝60°，∠B＝60°，∴∠C=60°，∴△ABC是等边三角形60°，故正确；
D根据有一个角是60°的等腰三角形是等边三角形可以得到，故正确.
故选B. 现有同一品牌工艺品100件,其中有2件次品,从中任取一件,( )是次品.
A. 一定 B. 不大可能
C. 很可能 D. 不可能
B
【解析】由于次品在总数中所占的数目较少,所以抽取一次,抽到次品的可能性较小.
故选B. 分式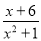
有意义的条件是____________
x可以取全体实数
【解析】试题解析：：因为恒大于0，所以x可以取全体实数.
故答案为：x可以取全体实数. 分式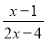
的值为零的条件是____________
【解析】试题解析：：因为分式的值为0的时候，只能是分子为0，分母不能为0，所以可以得到， ；可以得到且
故答案为： . 已知分式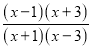
有意义，则x的取值为（ ）
A. x≠－1 B. x≠3 C. x≠－1且x≠3 D. x≠－1或x≠3
C
【解析】试题解析：分式的分母不能为0，所以， ，解得x≠－1且x≠3.
故选C. 计算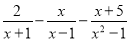
【解析】试题分析：先找出最简公分母，然后把各分式通分，然后按照分母不变，分子相加减的方法进行计算，最后把分子合并同类项，最后结果化成最简．
试题解析：
【解析】
原式＝
＝
＝． 分式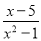
与
的公分母是（ ）
A. 
B. 
C. 
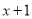D.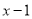 
A
【解析】试题分析：x2－1＝(x＋1)(x－1)，
所以分式与的公分母是(x＋1)(x－1)，
即x2－1．
故选A． 为进一步建设秀美、宜居的生态环境，某村欲购买甲、乙、丙三种树美化村庄，已知甲、乙丙三种树的价格之比为2：2：3，甲种树每棵200元，现计划用210000元资金，购买这三种树共1000棵．
（1）求乙、丙两种树每棵各多少元？
（2）若购买甲种树的棵树是乙种树的2倍，恰好用完计划资金，求这三种树各能购买多少棵？
（3）若又增加了10120元的购树款，在购买总棵树不变的前提下，求丙种树最多可以购买多少棵？
（1）200元，200元，（2）能购买甲种树600棵，乙种树300棵，丙种树100棵；（3）丙种树最多可以购买201棵．
【解析】
试题分析：（1）利用已知甲、乙丙三种树的价格之比为2：2：3，甲种树每棵200元，即可求出乙、丙两种树每棵钱数；
（2）假设购买乙种树x棵，则购买甲种树2x棵，丙种树（1000-3x）棵，利用（1）中所求树木价格以及现计划用210000元资金购买这三...