题目内容
【题目】在平面直角坐标系中,O为坐标原点,点A的坐标为(a,a),点B的坐标(b,c),且a、b、c满足![]() .
.
(1)若a没有平方根,判断点A在第几象限并说明理由.
(2)连AB、OA、OB,若△OAB的面积大于5而小于8,求a的取值范围;
(3)若两个动点M(2m,3m-5),N(n-1,-2n-3),请你探索是否存在以两个动点M、N为端点的线段MN∥AB,且MN=AB.若存在,求出M、N两点的坐标;若不存在,请说明理由.
【答案】(1)第三象限;(2)见解析;(3)见解析
【解析】
(1)根据平方根的意义得到a<0,然后根据各象限点的坐标点的特征可判断点A在第三象限;(2)先利用方程组![]() ,用a表示b、c,得b=2+a.c=a, 则B点的坐标为(2+a,a),故AB//x轴,AB=|2+a-a|=2,故
,用a表示b、c,得b=2+a.c=a, 则B点的坐标为(2+a,a),故AB//x轴,AB=|2+a-a|=2,故![]() 由若△OAB的面积大于5而小于8,可得
由若△OAB的面积大于5而小于8,可得![]() 计算即可得a的取值范围;
计算即可得a的取值范围;
(3)由AB//x轴即MN∥AB可得MN∥x轴,则M、N的y坐标,以及MN=AB=2,可得方程组解得m、n的值,即可得出结论;
(1)∵a没有平方根,
∴a<0,
∴点A在第三象限;
(2)解方程组![]()
用a表示b、c,得![]()
∵点B坐标为(b,c)
∴点B坐标为(2+a,a)
∵点A的坐标为(a,a)
∴AB=|2+a-a|=2,AB与x轴平行
∴![]()
∵△OAB的面积大于5而小于8,
∴![]()
解得:![]() 或
或![]()
(3) ∵AB∥x轴
又∵MN∥AB
∴MN∥x轴
∵M(2m, 3m-5) N(n-1, -2n-3), MN=AB=2
∴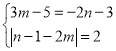
∴![]()
![]()
∴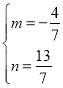 或
或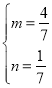
∴![]() 或
或![]()

【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共50个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸到球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的概率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计当![]() 很大时,摸到白球的频率将会接近______;(精确到0.1);
很大时,摸到白球的频率将会接近______;(精确到0.1);
(2)假如随机摸一次,摸到白球的概率P(白球)=______;
(3)试估算盒子里白色的球有多少个?