题目内容
15.如图,已知点C在线段AB上,且AM=$\frac{1}{3}$AC.BN=$\frac{1}{3}$BC
(1)若AC=12,CB=6,求线段MN的长;
(2)若点C为线段AB上任意一点,且满足AC+BC=a,请直接写出线段MN的长;
(3)如图2若点C为线段AB延长线上任意一点,且满足AC-CB=b,求线段MN的长.
分析 (1)根据AM=$\frac{1}{3}$AC.BN=$\frac{1}{3}$BC,可得AM的长,BN的长,根据线段的和差,可得答案;
(2)根据AM=$\frac{1}{3}$AC.BN=$\frac{1}{3}$BC,可得AM的长,BN的长,根据线段的和差,可得答案;
(3)根据AM=$\frac{1}{3}$AC.BN=$\frac{1}{3}$BC,可得MC的长,NC的长,根据线段的和差,可得答案.
解答 解:(1)由AM=$\frac{1}{3}$AC.BN=$\frac{1}{3}$BC,AC=12,CB=6,得
AM=$\frac{1}{3}$×12=4,BN=$\frac{1}{3}$×6=2.
由线段的和差,得
AB=AC+BC=12+6=18,
MN=AB-AM-NB=18-4-2=12;
(2)MN=AB-(AM+NB)=a-($\frac{1}{3}$AC+$\frac{1}{3}$BC)=a-$\frac{1}{3}$a=$\frac{2}{3}$a;
(3)由AM=$\frac{1}{3}$AC.BN=$\frac{1}{3}$BC,得
MC=AC-AM=$\frac{2}{3}$AC,NC=BC-BN=$\frac{2}{3}$BC.
MN=MC-NC=$\frac{2}{3}$AC-$\frac{2}{3}$BC=$\frac{2}{3}$(AC-BC)=$\frac{2}{3}$b.
点评 本题考查了两点间的距离,利用AM=$\frac{1}{3}$AC.BN=$\frac{1}{3}$BC,得出AM的长,BN的长是解题关键,又利用了线段的和差.

练习册系列答案
相关题目
5.关于矩形性质,下列说法不正确的是( )
| A. | 四个角都是直角 | |
| B. | 既是轴对称图形,也是中心对称图形 | |
| C. | 对角线互相垂直 | |
| D. | 对角线互相平分且相等 |
5.下列图案是中心对称图形的共有( )个


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
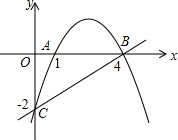 如图,抛物线经过三点A(1,0),B(4,0),C(0,-2).
如图,抛物线经过三点A(1,0),B(4,0),C(0,-2).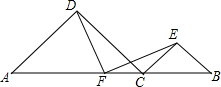 已知△ADC和△BCE均为等腰直角三角形,F是AB的中点,探究DF与EF的关系.
已知△ADC和△BCE均为等腰直角三角形,F是AB的中点,探究DF与EF的关系.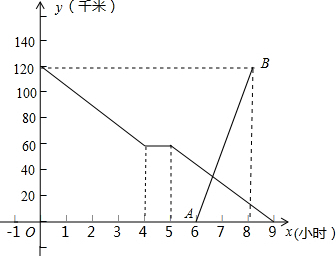 张老师骑自行车匀速从甲地到乙地,在途中休息了一段时间后,仍按原速行驶,他距乙地的距离与时间的关系如图中折线所示,李老师骑摩托车沿同一条路匀速从乙地到甲地,比张老师晚出发一段时间,他距乙地的距离与时间的关系如图中线段EF所示.
张老师骑自行车匀速从甲地到乙地,在途中休息了一段时间后,仍按原速行驶,他距乙地的距离与时间的关系如图中折线所示,李老师骑摩托车沿同一条路匀速从乙地到甲地,比张老师晚出发一段时间,他距乙地的距离与时间的关系如图中线段EF所示.
 如图,在平面直角坐标系中,矩形ABCO的面积为15,OA比OC大2,点E为BC的中点,以OE为直径的⊙O′交x轴于点D,过D作DF⊥EA.交AE于点F.
如图,在平面直角坐标系中,矩形ABCO的面积为15,OA比OC大2,点E为BC的中点,以OE为直径的⊙O′交x轴于点D,过D作DF⊥EA.交AE于点F.