��Ŀ����
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ᡢ
�ᡢ![]() ��ֱ��ཻ��
��ֱ��ཻ��![]() ��
��![]() ���㣬������
���㣬������![]()
![]() ������
������![]() ����
����![]() ���������ڵ�
���������ڵ�![]() ��
��
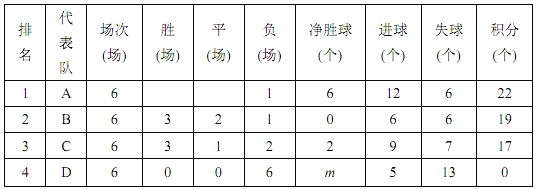
��1����������ߵĺ�������ʽ��
��2����֪��![]() ���������ϵ�һ�����㣬���ҵ�
���������ϵ�һ�����㣬���ҵ�![]() �ڵ�һ�����ڣ�����
�ڵ�һ�����ڣ�����![]() ��
��![]() �����
�����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ��
��![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() �ĺ�������ʽ�������
�ĺ�������ʽ�������![]() �����ֵ����ʱ����
�����ֵ����ʱ����![]() �����ꣻ
�����ꣻ
��3������![]() ��ԭ����ת�õ�
��ԭ����ת�õ�![]() ������
������![]() ��
��![]() ������ת�����У�һ����
������ת�����У�һ����![]() �ӵ�
�ӵ�![]() ���������߶�
���������߶�![]() ��ÿ��
��ÿ��![]() ����λ���ٶ��˶���
����λ���ٶ��˶���![]() �������߶�
�������߶�![]() ��ÿ��
��ÿ��![]() ����λ���ȵ��ٶ��˶���
����λ���ȵ��ٶ��˶���![]() ��ֹͣ�����
��ֹͣ�����![]() �������˶���������ʱ�����Ƕ��٣�
�������˶���������ʱ�����Ƕ��٣�
���𰸡���1��![]() ����2��
����2��![]() ��
��![]() �����ֵ��
�����ֵ��![]() ����ʱ����
����ʱ����![]() ��������
��������![]() ����3��
����3��![]() �룮
�룮
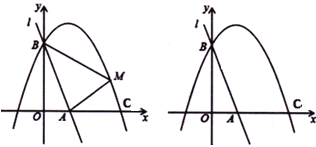
��������
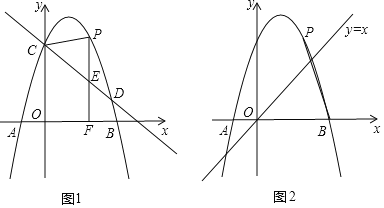
��1������ֱ��l�Ľ���ʽ�������B���꣬�ѵ�B�������![]() �����aֵ�����ɵ������߽���ʽ��
�����aֵ�����ɵ������߽���ʽ��
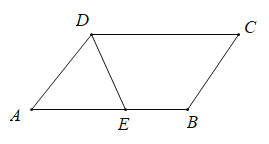
��2����ͼ������OM������M��ME��y����E��MD��x����D�����ݣ�1�������������߽���ʽ�������C���꣬�ɵó�m��ȡֵ��Χ������ֱ��l����ʽ�����A�����꣬����![]() ���ɵ�S����m�Ĺ�ϵʽ�����ö��κ��������ʼ������S�����ֵ�͵�M�����ꣻ
���ɵ�S����m�Ĺ�ϵʽ�����ö��κ��������ʼ������S�����ֵ�͵�M�����ꣻ
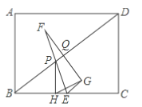
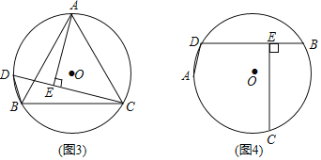
��3����ͼ��������������H��0��![]() ��������HA����OA����BA����CA������֤��
��������HA����OA����BA����CA������֤��![]() ���ɵ�
���ɵ�![]() ������
������![]() �����ù��ɶ������HC�ij����ɵõ�
�����ù��ɶ������HC�ij����ɵõ�![]() �������˶���������ʱ���ٵ�ʱ�䣮
�������˶���������ʱ���ٵ�ʱ�䣮
��1����![]() ����
����![]() ����
����![]() ��
��
���![]() ������Ϊ
������Ϊ![]() ��
��
��������![]()
![]() ������
������![]() ��
��
��![]() ��
��
��ã�![]() ��
��
�������ߵĽ���ʽΪ��![]() ��
��
��2����ͼ������OM������M��ME��y����E��MD��x����D��
��![]() ����
����![]() ����
����![]() ��
��![]() ��
��
���![]() ������Ϊ
������Ϊ![]() ��
��
�ߵ�![]() ���������ϵ�һ�����㣬���ҵ�
���������ϵ�һ�����㣬���ҵ�![]() ��һ�����ڣ���
��һ�����ڣ���![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ��
��
��![]() ����
����![]() ������Ϊ
������Ϊ![]() ��
��
��![]() ����
����![]() ����
����![]() ��
��
���![]() ������
������![]() ��
��
��![]()
![]()
=![]() OB��ME+
OB��ME+![]() OA��MD-
OA��MD-![]() OB��OA
OB��OA
![]() ��
��
����ã�![]() ��
��
��![]() ʱ��-m2+2m+3=
ʱ��-m2+2m+3=![]() ��
��
��![]() ʱ��
ʱ��![]() ȡ�����ֵ��
ȡ�����ֵ��![]() �����ֵ��
�����ֵ��![]() ����ʱ����
����ʱ����![]() ��������
��������![]() ��
��
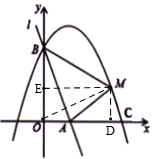
��3����ͼ��ȡ��![]() ������Ϊ
������Ϊ![]() ������
������![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]()
��![]() ��
��
��![]() ����
����![]() ��
��
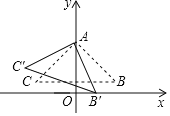
�ߵ�P��BA�����˶����ٶ���ÿ��3����λ���ȣ���CA�����˶����ٶ���ÿ��1����λ���ȣ�
����BA�����˶���ʱ��Ϊ![]() ����CA�����˶���ʱ��ΪA��C��
����CA�����˶���ʱ��ΪA��C��
��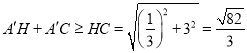 ��
��
���![]() �������˶���������ʱ
�������˶���������ʱ![]() ������
������![]() �������˶���������ʱ������
�������˶���������ʱ������![]() �룮
�룮

 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�