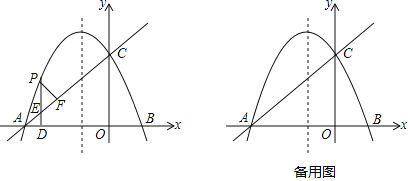题目内容
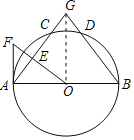
【题目】如图，AB是⊙O的直径，C、D为⊙O上两点，且
，过点O作OE⊥AC于点E⊙O的切线AF交OE的延长线于点F，弦AC、BD的延长线交于点G.
（1）求证：∠F＝∠B；
（2）若AB＝12，BG＝10，求AF的长.
【答案】（1）见解析；（2）
.
【解析】
（1）根据圆周角定理得到∠GAB＝∠B，根据切线的性质得到∠GAB+∠GAF＝90°，证明∠F＝∠GAB，等量代换即可证明；
（2）连接OG，根据勾股定理求出OG，证明△FAO∽△BOG，根据相似三角形的性质列出比例式，计算即可.
（1）证明：∵
，
∴
.
∴∠GAB＝∠B，
∵AF是⊙O的切线，
∴AF⊥AO.
∴∠GAB+∠GAF＝90°.
∵OE⊥AC，
∴∠F+∠GAF＝90°.
∴∠F＝∠GAB，
∴∠F＝∠B；
（2）解：连接OG.
∵∠GAB＝∠B，
∴AG＝BG.
∵OA＝OB＝6，
∴OG⊥AB.
∴
，
∵∠FAO＝∠BOG＝90°，∠F＝∠B，
∴△FAO∽△BOG，
∴
.
∴
.
【题目】地球环境问题已经成为我们日益关注的问题.学校为了普及生态环保知识，提高学生生态环境保护意识，举办了“我参与，我环保”的知识竞赛.以下是从初一、初二两个年级随机抽取20名同学的测试成绩进行调查分析，成绩如下：
初一：76 88 93 65 78 94 89 68 95 50
89 88 89 89 77 94 87 88 92 91
初二：74 97 96 89 98 74 69 76 72 78
99 72 97 76 99 74 99 73 98 74
（1）根据上面的数据，将下列表格补充完整；
整理、描述数据：
成绩x 人数 班级 |
|
|
|
|
|
初一 | 1 | 2 | 3 | 6 | |
初二 | 0 | 1 | 10 | 1 | 8 |
（说明：成绩90分及以上为优秀，80～90分为良好，60～80分为合格，60分以下为不合格）
分析数据：
年级 | 平均数 | 中位数 | 众数 |
初一 | 84 | 88.5 | |
初二 | 84.2 | 74 |
（2）得出结论：
你认为哪个年级掌握生态环保知识水平较好并说明理由.（至少从两个不同的角度说明推断的合理性）.
