Question

【题目】如图，已知抛物线y＝ax2+x+4的对称轴是直线x＝3，且与x轴交于A、B两点（点B在点A的右侧），与y轴交于点C．

（1）求抛物线的解析式；

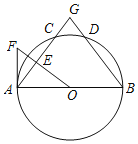
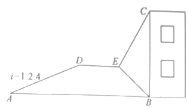
（2）以BC为边作正方形CBDE，求对角线BE所在直线的解析式；

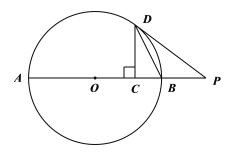
（3）点P是抛物线上一点，若∠APB＝45°，求出点P的坐标．

Answer 1

【答案】（1）y＝x+4；（2）y＝﹣3x+24或y＝；（3）点P坐标为（﹣4，﹣6）或（10，﹣6）.

【解析】

（1）利用对称轴公式列式即求出a的值，进而得抛物线解析式．

（2）由于边DE所在位置不同，故需对点E所在位置分类讨论．过点E作y轴垂线，根据∠BCE＝90°构造模型，即求得点E坐标，进而求直线BE解析式．

（3）由点P运动过程中∠APB＝45°联想到圆周上的圆周角，只要构造出∠APB为圆周角，其所对圆心角等于90°即可．故以AB为斜边作等腰直角三角形ABG．若G在第一象限，则圆与抛物线无除A、B外的交点，故点G需在第四象限．求出点G坐标，设P坐标，以PG的长等于半径5为等量关系列方程，即求得p的值进而得点P坐标．

解：（1）∵抛物线的对称轴是直线x＝3，

∴＝3，解得：a＝﹣，

∴抛物线的解析式为y＝﹣x2+x+4；

（2）当y＝﹣x2+x+4＝0时，解得：x1＝﹣2，x2＝8，

∴A（﹣2，0），B（8，0），

∴AB＝10，OB＝8，

当x＝0时，y＝﹣x2+x+4＝4，

∴C（0，4），OC＝4，

①如图1，若点E在第一象限，过点E作EF⊥y轴于点F，

∴∠CFE＝∠BOC＝90°，

∵四边形CBDE是正方形，

∴∠BCE＝90°，BC＝CE，

∴∠BCO+∠OBC＝∠BCO+∠FCE＝90°，

∴∠OBC＝∠FCE，

在△FCE与△OBC中

，

∴△FCE≌△OBC（AAS），

∴FC＝OB＝8，EF＝OC＝4，

∴OF＝OC+FC＝12，

∴E（4，12），

设直线BE解析式为：y＝kx+b，

∴，解得：，

∴直线BE解析式为y＝﹣3x+24，

②如图2，若点E在第三象限，过点E作EF⊥y轴于点F，

同理可证：△FCE≌△OBC（AAS），

∴FC＝OB＝8，EF＝OC＝4，

∴OF＝FC﹣OC＝8﹣4＝4，

∴E（﹣4，﹣4），

设直线BE解析式为：y＝k'x+b'，

∴，解得：，

∴直线BE解析式为y＝x- ，

综上所述，直线BE解析式为y＝﹣3x+24或y＝x-；

（3）以AB为斜边作等腰Rt△AGB，则AG＝BG，∠AGB＝90°，

以点G为圆心、AG长为半径画圆，则点P在优弧AB上时总有∠APB＝45°，

如图3，若点G在第一象限，⊙G与抛物线交点只有A、B，即没有满足条件的点P使∠APB＝45°，

如图4，若点G在第四象限，过点G作GM⊥x轴于点M，

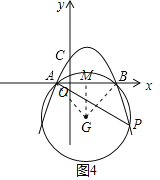
∴AM＝BM＝GM＝AB＝5，

∴G（3，﹣5），

设P（p，-p2+p+4），

∵PG＝AG＝AB＝5，

∴PG2＝50 可得方程：（p﹣3）2+（-p2+p+4+5）2＝50，

解得：p1＝﹣4，p2＝10，p3＝﹣2（即点A，舍去），p4＝8（即点B，舍去），

∴-p2+p+4＝﹣6，

∴点P坐标为（﹣4，﹣6）或（10，﹣6）.

故答案为：（1）y＝x+4；（2）y＝﹣3x+24或y＝；（3）点P坐标为（﹣4，﹣6）或（10，﹣6）.