题目内容
 等腰直角三角形AOB中腰OA=OB=6,将它放在一个平面直角坐标系内,如图所示,已知点P是AB边上一动点,点Q是OA边上的定点,OQ=4.设点P的坐标是(x,y),△OPQ的面积为S.
等腰直角三角形AOB中腰OA=OB=6,将它放在一个平面直角坐标系内,如图所示,已知点P是AB边上一动点,点Q是OA边上的定点,OQ=4.设点P的坐标是(x,y),△OPQ的面积为S.(1)求y与x的函数关系式;
(2)求S与x的函数关系式,并求出当S=10时,点P的坐标.
分析:(1)作PC⊥x轴于点C,根据点P(x,y)可知OC=x,PC=y.∠PCA=90°,因为△AOB是等腰直角三角形,所以∠OAB=45°即∠PAC=45°,故可得出PC=CA=y,由OA+CA=6可知x+y=6,由此即可得出结论;
(2)直接根据三角形的面积公式求出S与x的关系式,再把S=10代入求出x的值,进而可得出y的值,由此可得出P点坐标.
(2)直接根据三角形的面积公式求出S与x的关系式,再把S=10代入求出x的值,进而可得出y的值,由此可得出P点坐标.
解答: 解:(1)作PC⊥x轴于点C,
解:(1)作PC⊥x轴于点C,
∵点P(x,y),
∴OC=x,PC=y.∠PCA=90°,
∵△AOB是等腰直角三角形
∴∠OAB=45°即∠PAC=45°,
∴∠CPA=∠CAP=45°
∴PC=CA=y,
∵OA+CA=6即x+y=6,
∴y与x的函数关系式为y=6-x(0<x<6);
(2)∵S=
OQ•PC=
×4×y=
×4×(6-x)=12-2x,
∴当S=10时,即10=12-2x,解得x=1,此时y=6-1=5,
∴此时点P的坐标为(1,5).
 解:(1)作PC⊥x轴于点C,
解:(1)作PC⊥x轴于点C,∵点P(x,y),
∴OC=x,PC=y.∠PCA=90°,
∵△AOB是等腰直角三角形
∴∠OAB=45°即∠PAC=45°,
∴∠CPA=∠CAP=45°
∴PC=CA=y,
∵OA+CA=6即x+y=6,
∴y与x的函数关系式为y=6-x(0<x<6);
(2)∵S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴当S=10时,即10=12-2x,解得x=1,此时y=6-1=5,
∴此时点P的坐标为(1,5).
点评:本题考查的是一次函数综合题,涉及到等腰直角三角形的性质及三角形的面积公式等知识,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
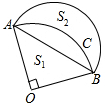 如图,等腰直角三角形AOB的面积为S1,以点O为圆心,OA为半径的弧与以AB为直径的半圆围成的图形的面积为S2,则S1与S2的关系是( )
如图,等腰直角三角形AOB的面积为S1,以点O为圆心,OA为半径的弧与以AB为直径的半圆围成的图形的面积为S2,则S1与S2的关系是( )| A、S1>S2 | B、S1<S2 | C、S1=S2 | D、S1≥S2 |
 17、正方形ABCD中对角线AC、BD相交于点O,设E是OB上的一点,DF⊥AE与F,交OA于G,等腰直角三角形△AOB≌△BOC≌△COD≌△DOA;等腰直角三角形△ABC≌△BCD≌△CDA≌△DAB.除此之外再写出三对你认为全等的三角形它们是:
17、正方形ABCD中对角线AC、BD相交于点O,设E是OB上的一点,DF⊥AE与F,交OA于G,等腰直角三角形△AOB≌△BOC≌△COD≌△DOA;等腰直角三角形△ABC≌△BCD≌△CDA≌△DAB.除此之外再写出三对你认为全等的三角形它们是: (2013•滨湖区二模)如图,已知点A是双曲线y=
(2013•滨湖区二模)如图,已知点A是双曲线y=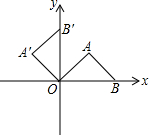 将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为
将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为