��Ŀ����
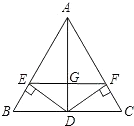
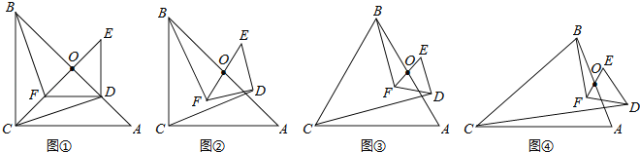
����Ŀ����ͼ������ABC����DEF���ǵ���ֱ�������Σ���ACB=��EDF=90�㣬�ҵ�D��AB���ϣ�AB��EF���е��ΪO������BF��CD��CO����Ȼ��C��F��O��ͬһ��ֱ���ϣ�����֤����BOF�ա�COD����BF=CD��
�������
��1����ͼ���е�Rt��DEF�Ƶ�O��ת�õ�ͼ���������ʱ�߶�BF��CD��������ϵ����֤����Ľ��ۣ�
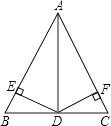
��2����ͼ��������ABC����DEF���ǵȱ������Σ�AB��EF���е��ΪO��������1���еĽ�����Ȼ�����������������˵�����ɣ��粻�����������BF��CD֮���������ϵ��
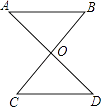
��3����ͼ��������ABC����DEF���ǵ��������Σ�AB��EF���е��Ϊ0���Ҷ�����ACB=��EDF=������ֱ��д��![]() ��ֵ���ú�����ʽ�ӱ�ʾ������
��ֵ���ú�����ʽ�ӱ�ʾ������
���𰸡���1�� BF=CD��֤������������2����1���еĽ��۲����������ɼ���������3��![]() =tan
=tan![]() ��
��
��������
�����������1�����ͼ����ʾ������OC��OD��֤����BOF�ա�COD��
��2�����ͼ����ʾ������OC��OD��֤����BOF�ס�COD�����Ʊ�Ϊ![]() ��
��
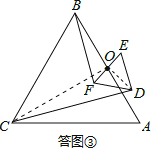
��3�����ͼ����ʾ������OC��OD��֤����BOF�ס�COD�����Ʊ�Ϊtan![]() ��
��
�����������1�����룺BF=CD���������£�
���ͼ����ʾ������OC��OD��
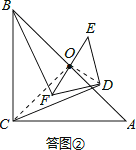
�ߡ�ABCΪ����ֱ�������Σ���OΪб��AB���е㣬
��OB=OC����BOC=90����
�ߡ�DEFΪ����ֱ�������Σ���OΪб��EF���е㣬
��OF=OD����DOF=90����
�ߡ�BOF=��BOC+��COF=90��+��COF����COD=��DOF+��COF=90��+��COF��
���BOF=��COD��
������BOF����COD��
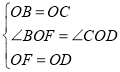
���BOF�ա�COD��SAS����
��BF=CD��
��2������1���еĽ��۲�������
���ͼ����ʾ������OC��OD��
�ߡ�ABCΪ�ȱ������Σ���OΪ��AB���е㣬
��![]() =tan30��=
=tan30��=![]() ����BOC=90����
����BOC=90����
�ߡ�DEFΪ�ȱ������Σ���OΪ��EF���е㣬
��![]() =tan30��=
=tan30��=![]() ����DOF=90����
����DOF=90����
��![]() ��
��
�ߡ�BOF=��BOC+��COF=90��+��COF����COD=��DOF+��COF=90��+��COF��
���BOF=��COD��
����BOF����COD��
��![]() ����BOF=��COD��
����BOF=��COD��
���BOF�ס�COD��
��![]()
��3�����ͼ����ʾ������OC��OD��
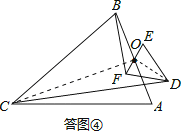
�ߡ�ABCΪ���������Σ���OΪ�ױ�AB���е㣬
��![]() =tan
=tan![]() ����BOC=90����
����BOC=90����
�ߡ�DEFΪ���������Σ���OΪ�ױ�EF���е㣬
��![]() =tan
=tan![]() ����DOF=90����
����DOF=90����
��![]() =
=![]() =tan
=tan![]()
�ߡ�BOF=��BOC+��COF=90��+��COF����COD=��DOF+��COF=90��+��COF��
���BOF=��COD��
����BOF����COD��
��![]() =
=![]() =tan
=tan![]() ����BOF=��COD��
����BOF=��COD��
���BOF�ס�COD��
��![]() =tan
=tan![]() ��
��