题目内容
17．解方程（1）$\frac{3x-5}{x-2}$=2+$\frac{x+1}{2-x}$
（2）$\frac{2}{3}$+$\frac{x}{3x-1}$=$\frac{1}{9x-3}$．
分析 两分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答 解：（1）去分母得：3x-5=2x-4-x-1，
解得：x=0，
经检验x=0是分式方程的解；
（2）去分母得：6x-2+3x=1，
解得：x=$\frac{1}{3}$，
经检验x=$\frac{1}{3}$是增根，分式方程无解．
点评 此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．
练习册系列答案
相关题目
15．化简$\frac{2x}{{x}^{2}+2x}$-$\frac{x-6}{{x}^{2}-4}$的结果为（ ）
| A． | $\frac{1}{{x}^{2}-4}$ | B． | $\frac{1}{{x}^{2}+2x}$ | C． | $\frac{1}{x-2}$ | D． | $\frac{x-6}{x-2}$ |
5．下列说法中，正确的是（ ）
| A． | 两条直线被第三条直线所截，同位角相等 | |
| B． | 联结直线外一点到直线上各点的所有线段中，垂线最短 | |
| C． | 经过一点，有且只有一条直线与已知直线平行 | |
| D． | 在同一平面内，经过一点，有且只有一条直线与已知直线垂直 |
已知：如图，等腰△ABC中，AB=AC，BD、CE分别是边AC、AB上的中线，BD与CE相交于点O，点M、N分别为线段BO和CO中点．求证：四边形EDNM是矩形．
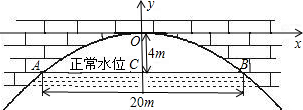如图，有一抛物线形拱桥，正常水位时桥下水面宽20m，拱顶距离水面4m．已知其抛物线解析式为y=-0.04x2，在正常水位时，桥下的水深为2m，为保证过往船只顺利通行，桥下水面的宽度不得小于18m，求水深超过多少米时，就会影响过往船只从桥下顺利通行？