题目内容
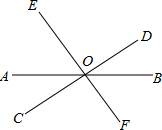如图，三条直线AB，CD，EF相交于同一点O，若∠AOE=2∠AOC，∠COF比∠AOE大30°，求∠AOC的度数．
解：∵∠AOE=2∠AOC，∠COF比∠AOE大30°，
∴∠COF=∠AOE+30°=2∠AOC+30°，
∵∠AOC+∠AOE+∠COF=180°，
∴∠AOC+2∠AOC+2∠AOC+30°=180°，
解得∠AOC=30°．
分析：根据题意用∠AOC表示出∠COF，然后根据平角等于180°列式计算即可得解．
点评：本题考查了邻补角，根据题意，利用平角等于180°列出关于∠AOC的方程是解题的关键．
∴∠COF=∠AOE+30°=2∠AOC+30°，
∵∠AOC+∠AOE+∠COF=180°，
∴∠AOC+2∠AOC+2∠AOC+30°=180°，
解得∠AOC=30°．
分析：根据题意用∠AOC表示出∠COF，然后根据平角等于180°列式计算即可得解．
点评：本题考查了邻补角，根据题意，利用平角等于180°列出关于∠AOC的方程是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
25、已知：如图，三条直线AB，CD，EF相交于O，且CD⊥EF，∠AOC=20°，若OG平分∠BOF．求∠DOG．
如图，三条直线AB、CD、EF相交于同一点O，若∠AOE=2∠AOC，∠COF=60°，求∠BOD的度数．
如图，三条直线AB，CD，EF相交于点O，若∠AOD=3∠FOD，∠AOE=120°，则∠FOD的度数为（ ）
如图，三条直线AB、CD、EF交于点O，则图中以O为顶点的角（包括平角）共有（ ）
如图，三条直线AB，CD，EF相交于同一点O，若∠AOE=2∠AOC，∠COF比∠AOE大30°，求∠AOC的度数．