题目内容
Rt△ABC三边分别为a、b、c,且a、b满足
+b2-8b+16=0,求Rt△ABC的面积.
| 3-a |
分析:先根据完全平方公式整理,利用非负数的性质列式求解得到a、b的值,再分a是直角边和斜边两种情况,利用勾股定理求出另一直角边,然后根据三角形的面积公式列式计算即可得解.
解答:解:
+b2-8b+16=0,
配方得,
+(b-4)2=0,
所以,3-a=0,b-4=0,
解得a=3,b=4;
b=4是直角边时,3是直角边,△ABC的面积=
×3×4=6;
b=4是斜边时,另一直角边=
=
,
△ABC的面积=
×
×3=
,
综上所述,Rt△ABC的面积为6或
.
| 3-a |
配方得,
| 3-a |
所以,3-a=0,b-4=0,
解得a=3,b=4;
b=4是直角边时,3是直角边,△ABC的面积=
| 1 |
| 2 |
b=4是斜边时,另一直角边=
| 42-32 |
| 7 |
△ABC的面积=
| 1 |
| 2 |
| 7 |
3
| ||
| 2 |
综上所述,Rt△ABC的面积为6或
3
| ||
| 2 |
点评:本题考查了二次根式的应用,非负数的性质,配方法的应用以及勾股定理,难点在于要分情况讨论.

练习册系列答案
相关题目
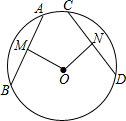 小雅同学在学习圆的基本性质时发现了一个结论:如图,在⊙O中,OM⊥弦AB于点M,ON⊥弦CD于点N,若OM=ON,则AB=CD.
小雅同学在学习圆的基本性质时发现了一个结论:如图,在⊙O中,OM⊥弦AB于点M,ON⊥弦CD于点N,若OM=ON,则AB=CD. (2011•武汉模拟)小雅同学在学习圆的基本性质时发现了一个结论:如图,⊙O中,OM⊥弦AB于点M,ON⊥弦CD于点N,若OM=ON,则AB=CD.
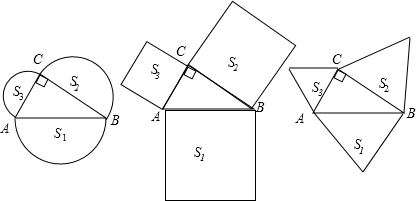
(2011•武汉模拟)小雅同学在学习圆的基本性质时发现了一个结论:如图,⊙O中,OM⊥弦AB于点M,ON⊥弦CD于点N,若OM=ON,则AB=CD. 如图,分别以Rt△ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,容易得出S1、S2、S3之间有的关系式
如图,分别以Rt△ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,容易得出S1、S2、S3之间有的关系式