题目内容
 如图所示,∠AOB是直角,∠AOC是锐角,ON是∠AOC的角平分线,OM是∠BOC的角平分线;
如图所示,∠AOB是直角,∠AOC是锐角,ON是∠AOC的角平分线,OM是∠BOC的角平分线;(1)如果∠AOC=60°时,∠MON=
45°
45°
;(2)如果∠AOC=50°时,∠MON=
45°
45°
;(3)设∠AOC=x°时,利用你学过的一元一次方程思想,求∠MON的度数.你发现了(证明)一个什么规律?
分析:(1)先可以求出∠BOC=90°+60°=150°,由角平分线的性质就可以得出∠MOC=75°及∠NOC=30°的值就可以求出∠MON的值;
(2)先可以求出∠BOC=90°+50°=140°,由角平分线的性质就可以得出∠MOC=70°及∠NOC=25°的值就可以求出∠MON的值;
(3)先可以求出∠BOC=90°+x°=45°+0.5x°,由角平分线的性质就可以得出∠MOC=45°及∠NOC=0.5x°的值就可以求出∠MON的值;
(2)先可以求出∠BOC=90°+50°=140°,由角平分线的性质就可以得出∠MOC=70°及∠NOC=25°的值就可以求出∠MON的值;
(3)先可以求出∠BOC=90°+x°=45°+0.5x°,由角平分线的性质就可以得出∠MOC=45°及∠NOC=0.5x°的值就可以求出∠MON的值;
解答: 解:(1)∵∠AOB=90°,∠AOC=60°,
解:(1)∵∠AOB=90°,∠AOC=60°,
∴∠AOB+∠AOC=∠BOC=150°.
∵OM平分∠BOC,
∴∠MOC=
∠BOC=75°.
∵ON是∠AOC的角平分线,
∴∠1=
∠AOC=30°.
∴∠MOC-∠1=75°-30°=45°.
即∠MON=45°;
(2))∵∠AOB=90°,∠AOC=50°,
∴∠AOB+∠AOC=∠BOC=140°.
∵OM平分∠BOC,
∴∠MOC=
∠BOC=70°.
∵ON是∠AOC的角平分线,
∴∠1=
∠AOC=25°.
∴∠MOC-∠1=70°-25°=45°.
即∠MON=45°;
(3))∵∠AOB=90°,∠AOC=x°,
∴∠AOB+∠AOC=∠BOC=90°+x°.
∵OM平分∠BOC,
∴∠MOC=
∠BOC=45°+0.5x°.
∵ON是∠AOC的角平分线,
∴∠1=
∠AOC=0.5x°.
∴∠MOC-∠1=45°+0.5x°-0.5x°=45°.
即∠MON=45°;
故答案为:45°,45°,∠MON的度数不变.
 解:(1)∵∠AOB=90°,∠AOC=60°,
解:(1)∵∠AOB=90°,∠AOC=60°,∴∠AOB+∠AOC=∠BOC=150°.
∵OM平分∠BOC,
∴∠MOC=
| 1 |
| 2 |
∵ON是∠AOC的角平分线,
∴∠1=
| 1 |
| 2 |
∴∠MOC-∠1=75°-30°=45°.
即∠MON=45°;
(2))∵∠AOB=90°,∠AOC=50°,
∴∠AOB+∠AOC=∠BOC=140°.
∵OM平分∠BOC,
∴∠MOC=
| 1 |
| 2 |
∵ON是∠AOC的角平分线,
∴∠1=
| 1 |
| 2 |
∴∠MOC-∠1=70°-25°=45°.
即∠MON=45°;
(3))∵∠AOB=90°,∠AOC=x°,
∴∠AOB+∠AOC=∠BOC=90°+x°.
∵OM平分∠BOC,
∴∠MOC=
| 1 |
| 2 |
∵ON是∠AOC的角平分线,
∴∠1=
| 1 |
| 2 |
∴∠MOC-∠1=45°+0.5x°-0.5x°=45°.
即∠MON=45°;
故答案为:45°,45°,∠MON的度数不变.
点评:本题考查了一元一次方程的运用,角平分线的性质的运用,角的计算的运用,解答时合理运用角平分线的性质是关键.

练习册系列答案
相关题目
 18、如图所示,∠AOB是一个钢架,且∠AOB=10°,为了使钢架更加牢固,需在内部添加一些钢管EF、FG、GH …添加钢管的长度都与OE相等,则最多能添加这样的钢管的根数为( )
18、如图所示,∠AOB是一个钢架,且∠AOB=10°,为了使钢架更加牢固,需在内部添加一些钢管EF、FG、GH …添加钢管的长度都与OE相等,则最多能添加这样的钢管的根数为( )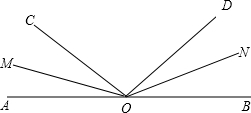 如图所示,∠AOB是平角,OM、ON分别是∠AOC、∠BOD的平分线.
如图所示,∠AOB是平角,OM、ON分别是∠AOC、∠BOD的平分线. 23、如图所示,∠AOB是平角,OC是射线,OD和OE分别是∠AOC,∠BOC的角平分线,你能求出∠DOE的度数吗?
23、如图所示,∠AOB是平角,OC是射线,OD和OE分别是∠AOC,∠BOC的角平分线,你能求出∠DOE的度数吗? 如图所示,∠AOB是平角,OC是射线,OD、OE分别是∠AOC、∠BOC的角平分线,若∠AOD=65°,求∠DOE和∠BOE的度数.
如图所示,∠AOB是平角,OC是射线,OD、OE分别是∠AOC、∠BOC的角平分线,若∠AOD=65°,求∠DOE和∠BOE的度数. 如图所示,∠AOB是一个钢架,且∠AOB=10°,为了使钢架更加牢固,需在内部添加一些钢管EF,FG,GH,…,添加的钢管长度都与0E相等,则最多能添加这样的钢管
如图所示,∠AOB是一个钢架,且∠AOB=10°,为了使钢架更加牢固,需在内部添加一些钢管EF,FG,GH,…,添加的钢管长度都与0E相等,则最多能添加这样的钢管