题目内容

3．已知等边三角形的面积为4$\sqrt{3}$，则它的边长为（　　）
A．6B．5C．4D．3

分析 作出等边三角形边上高，利用60°的正弦值可表示出高的值，利用三角形的面积公式求解即可．

解答 解：如图，作AD⊥BC于点D．
设AB=BC=AC=x，
则AD=AB×sin∠B=$\frac{\sqrt{3}}{2}$x，
故边长为x的等边三角形的面积为$\frac{1}{2}$×x×$\frac{\sqrt{3}}{2}$x=4$\sqrt{3}$，
解得：x=4，
故选：C．

点评 此题主要考查了三角形的面积的求法；利用60°的正弦值表示出等边三角形一边上的高是解决本题的突破点．

练习册系列答案
相关题目
18．如图是九（1）班45名同学每周课外阅读时间的频数直方图（每组含前一个边界值，不含后一个边界值）．由图可知，人数最多的一组是（　　）
A．2～4小时B．4～6小时C．6～8小时D．8～10小时
19．因式分解：6x2-3x=3x（2x-1）．
11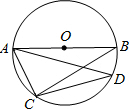．如图，AB是⊙O的直径，∠ADC=30°，OA=2，则AC的长为（　　）
A．2B．4C．$2\sqrt{3}$D．$\sqrt{3}$
18．若3m=5，3n=2，则3m+n的值是（　　）
A．10B．7C．5D．3
8．若2m=3，2n=4，则23m-2n的值为（　　）
A．$\frac{16}{27}$B．$\frac{9}{8}$C．$\frac{8}{27}$D．$\frac{27}{16}$
15．我们可以通过类比联想，引申拓展研究典型题目，可达到解一题知一类的目的，下面是一个案例，请补充完整
原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，试说明理由．

（1）思路梳理
∵AB=AD，
∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合．
∵∠ADC=∠B=90°，
∴∠FDG=180°，点F、D、G共线．
根据SAS，易证△AFG≌△AFG，得EF=BE+DF．
（2）类比引申
如图2，四边形ABCD中，AB=AD，∠BAD=90°点E、F分别在边BC、CD上，∠EAF=45°．若∠B、∠D都不是直角，则当∠B与∠D满足等量关系∠B+∠D=180°时，仍有EF=BE+DF．
（3）联想拓展
如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°．猜想BD、DE、EC应满足的等量关系，并写出推理过程．
12．如图，矩形ABCD中，对角线AC的垂直平分线分别交AB、DC于点E、F，连接AF，已知AD=4，AF=5，则AB的长（　　）
A．6B．7C．8D．9
13．已知某种纸一张的厚度约为0.0089cm，用科学记数法表示这个数为（　　）
A．8.9×103B．8.9×10-4C．8.9×10-3D．89×10-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网