题目内容
 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.(1)求证:CB∥PD.
(2)若BC=5,sinP=
| 5 |
| 13 |
考点:圆周角定理,解直角三角形
专题:
分析:(1)根据同弧所对的圆周角相等可得∠C=∠P,然后根据∠1=∠C,可得∠1=∠P,即可判断CB∥PD;
(2)连接AC,证明∠A=∠P,然后利用三角函数求出直径AB的长度,继而可得出半径.
(2)连接AC,证明∠A=∠P,然后利用三角函数求出直径AB的长度,继而可得出半径.
解答: (1)证明:∵∠C与∠P是
(1)证明:∵∠C与∠P是
所对的圆周角,
∴∠BCD=∠P,
又∵∠1=∠C,
∴∠1=∠P,
∴CB∥PD;
(2)解:连接AC.
∵AB为0D的直径,
∴∠ACB=90°.
又∵CD⊥AB,
∴
=
,
∴∠A=∠P,
∴sin∠A=sin∠P=
,
在Rt△ABC中,
∵BC=5,sin∠A=
=
,
∴AB=13,
则⊙O的半径为6.5.
 (1)证明:∵∠C与∠P是
(1)证明:∵∠C与∠P是 |
| BD |
∴∠BCD=∠P,
又∵∠1=∠C,
∴∠1=∠P,
∴CB∥PD;
(2)解:连接AC.
∵AB为0D的直径,
∴∠ACB=90°.
又∵CD⊥AB,
∴
 |
| BC |
 |
| BD |
∴∠A=∠P,
∴sin∠A=sin∠P=
| 5 |
| 13 |
在Rt△ABC中,
∵BC=5,sin∠A=
| BC |
| AB |
| 5 |
| 13 |
∴AB=13,
则⊙O的半径为6.5.
点评:本题考查了圆周角定理,注意掌握在同圆或等圆中,相等的弧所对的圆周角相等,直径所对的圆周角为直角;垂直于弦的直径平分弦,并且平分弦所对的弧.

练习册系列答案
相关题目
下列方程变形中,正确的是( )
A、由
| ||||
B、由-2x=3,得x=-
| ||||
C、由5x=-4,得x=-
| ||||
D、由
|
已知x=-2是方程a(x+1)=2a(x-1)+5的解,那么a等于( )
| A、1 | B、-1 | C、0 | D、5 |
已知y=mxm-2是反比例函数,则m的值是( )
| A、m≠0 | B、m=-1 |
| C、m=1 | D、m=2 |
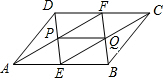 如图,E、F分别是?ABCD的两边AB、CD的中点,AF交DE于P,BF交CE于Q,则PQ与AB的关系是( )
如图,E、F分别是?ABCD的两边AB、CD的中点,AF交DE于P,BF交CE于Q,则PQ与AB的关系是( )| A、PQ∥AB | ||
B、PQ=
| ||
C、PQ∥AB且PQ=
| ||
| D、随?ABCD的形状大小变化而变化 |
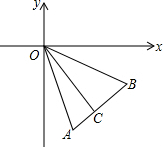 如图,在平面直角坐标系中,A、B两点分别位于第四象限,且∠AOB=45°,OC⊥AB于C,把△AOC沿直线OA翻折后,OC边恰好落在y轴上,若AC=1,OC=3,求经过点A的双曲线和B点坐标.
如图,在平面直角坐标系中,A、B两点分别位于第四象限,且∠AOB=45°,OC⊥AB于C,把△AOC沿直线OA翻折后,OC边恰好落在y轴上,若AC=1,OC=3,求经过点A的双曲线和B点坐标.