题目内容
方程x2+18x+30=2| x2+18x+45 |
分析:先将
看成一个整体a,则原方程变为a2-2a-15=0,解得a=5或a=-3(不合题意舍去)则x2+18x+45=25,即x2+18x+20=0,由此得到x1+x2=-18,x1•x2=20,然后代入所求代数式即可求出其值.
| x2+18x+45 |
解答:解:设
=a,
则原方程变为a2-2a-15=0,
解得a=5或a=-3(不合题意舍去),
则x2+18x+45=25,即x2+18x+20=0,
设方程的两根分别为x1,x2,
又由根与系数的关系可知:
x1+x2=-18,x1•x2=20;
∴原方程的实根倒数和=
=-
.
故填空答案为-
.
| x2+18x+45 |
则原方程变为a2-2a-15=0,
解得a=5或a=-3(不合题意舍去),
则x2+18x+45=25,即x2+18x+20=0,
设方程的两根分别为x1,x2,
又由根与系数的关系可知:
x1+x2=-18,x1•x2=20;
∴原方程的实根倒数和=
| x1+x2 |
| x1x2 |
| 9 |
| 10 |
故填空答案为-
| 9 |
| 10 |
点评:本题考查一元二次方程根与系数的关系,根据方程的特点,利用换元法把原方程转化为关于x的一元二次方程,利用根与系数的关系解决问题.

练习册系列答案
相关题目
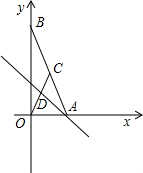 已知:如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(OA<OB)是方程x2-18x+72=0的两个根,点C是线段AB的中点,点D在线段OC上,且OD=2CD.
已知:如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(OA<OB)是方程x2-18x+72=0的两个根,点C是线段AB的中点,点D在线段OC上,且OD=2CD. 的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.
的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.