题目内容
 如图,大小两个正方形边长分别为a、b.
如图,大小两个正方形边长分别为a、b.(1)用含a、b的代数式阴影部分的面积S;
(2)如果a+b=7,ab=5,求阴影部分的面积.
考点:整式的混合运算,整式的混合运算—化简求值
专题:
分析:(1)利用整体面积减去空白面积得出阴影部分面积求出即可;
(2)利用完全平方公式结合已知条件求出即可.
(2)利用完全平方公式结合已知条件求出即可.
解答:解:(1)∵大小两个正方形边长分别为a、b,
∴阴影部分的面积为:S=a2+b2-
a2-
(a+b)b=
a2+
b2-
ab;
(2)∵a+b=7,ab=5,
∴
a2+
b2-
ab=
(a+b)2-
ab=
×72-
×5=17.
∴阴影部分的面积为:S=a2+b2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵a+b=7,ab=5,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
点评:此题主要考查了整式的混合运算以及化简求值,正确利用整体面积减去空白面积得出阴影部分面积是解题关键.

练习册系列答案
相关题目
一元二次方程(m-2)x2-4mx+2m-6=0有两个相等的实数根,则m等于( )
| A、-6或1 | B、1 | C、-6 | D、2 |
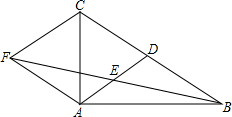 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.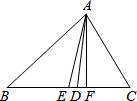 如图,在△ABC中,AE是中线,AD是角平分线,AF是高.则
如图,在△ABC中,AE是中线,AD是角平分线,AF是高.则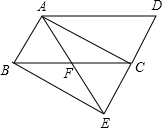 如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.