题目内容
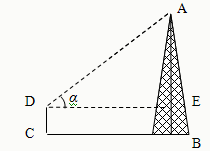
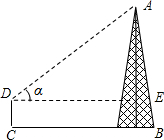 如图,小明为测量某铁塔AB的高度,他处测得塔顶的仰角已知小明的测角仪高CD=1.5米,求铁塔AB的高.(精确到0.1米(参考数据:sin43°=0.6820,cos43°=0.7314,tan43°=0.9325)
如图,小明为测量某铁塔AB的高度,他处测得塔顶的仰角已知小明的测角仪高CD=1.5米,求铁塔AB的高.(精确到0.1米(参考数据:sin43°=0.6820,cos43°=0.7314,tan43°=0.9325)
分析:易得四边形DCBE是矩形,即可求得EB=DC=1.5米,DE=CB=10米,然后在Rt△AED中,∠ADE=α=43°,利用∠ADE的正切函数即可求得AE的长,继而求得铁塔AB的高.
解答: 解:如图,过点D作DE⊥AB于E,
解:如图,过点D作DE⊥AB于E,
∵DC⊥BC,EB⊥BC,
∴∠C=∠CBE=∠BED=90°,
∴四边形DCBE是矩形,
∴EB=DC=1.5米,DE=CB=10米,
在Rt△AED中,∠ADE=α=43°
∵tanα=
,
∴AE=DEtan43°=10×0.9325=9.325,
∴AB=AE+EB=9.325+1.5=10.825≈10.8(米),
∴铁塔AB的高约是10.8米.
 解:如图,过点D作DE⊥AB于E,
解:如图,过点D作DE⊥AB于E,∵DC⊥BC,EB⊥BC,
∴∠C=∠CBE=∠BED=90°,
∴四边形DCBE是矩形,
∴EB=DC=1.5米,DE=CB=10米,
在Rt△AED中,∠ADE=α=43°
∵tanα=
| AE |
| DE |
∴AE=DEtan43°=10×0.9325=9.325,
∴AB=AE+EB=9.325+1.5=10.825≈10.8(米),
∴铁塔AB的高约是10.8米.
点评:此题考查了仰角的知识.要求学生能借助仰角构造直角三角形并解直角三角形,注意数形结合思想应用.

练习册系列答案
相关题目
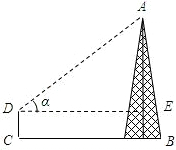 如图,小明为测量某铁塔AB的高度,他在离塔底B的10米C处测得塔顶的仰角α=43°,已知小明的测角仪高CD=1.5米,求铁塔AB的高.(精确到0.1米)
如图,小明为测量某铁塔AB的高度,他在离塔底B的10米C处测得塔顶的仰角α=43°,已知小明的测角仪高CD=1.5米,求铁塔AB的高.(精确到0.1米)