题目内容
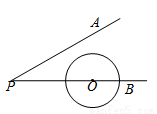
如图， 已知∠APB=300,圆心O在边PB上, ⊙O 的半径为1cm,OP=3cm. 若⊙O 沿射线BP方向平移，当 ⊙O 与直线PA相切时，圆心O平移的距离为_________cm．
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
提分百分百检测卷系列答案宝贝计划期末冲刺夺100分系列答案能考试全能100分系列答案题目内容
如图， 已知∠APB=300,圆心O在边PB上, ⊙O 的半径为1cm,OP=3cm. 若⊙O 沿射线BP方向平移，当 ⊙O 与直线PA相切时，圆心O平移的距离为_________cm．
提分百分百检测卷系列答案宝贝计划期末冲刺夺100分系列答案能考试全能100分系列答案
B. 
C. 
D. 
上，矩形的顶点均为动点，且矩形在抛物线与
轴围成的区域里。
， 
），试求矩形周长
关于变量
的函数表达式；
B. 
C. 
D. 
＝1
，则点B表示的数为 ．