题目内容
如图,Rt△OA1B1是由Rt△OAB绕点O顺时针方向旋转得到的,且A、O、B1三点共线.如果∠OAB=90°,∠AOB=30°,OA= .则图中阴影部分的面积为 .(结果保留π)
.则图中阴影部分的面积为 .(结果保留π)
【答案】分析:在直角△OAB中,利用三角函数即可求得AB、OA、OB的长度,求得△ABO的面积,扇形BOB′的面积,依据图中阴影部分的面积为:S扇形BOB′-S△OAB即可求解.
解答:解:∵Rt△OAB中∠OAB=90°,∠AOB=30°,OA= .
.
∴AB=OA•tan∠AOB= ×
× =1,OB=2,∠BOB′=180°-30°=150°,
=1,OB=2,∠BOB′=180°-30°=150°,
∴S△OAB= AB•OA=
AB•OA= ×1×
×1× =
= ,
,
S扇形BOB′= =
= π,
π,
则图中阴影部分的面积为 .
.
故答案是: .
.
点评:本题考查了扇形的面积公式,理解图中阴影部分的面积为:S扇形BOB′-S△OAB是解题的关键.
解答:解:∵Rt△OAB中∠OAB=90°,∠AOB=30°,OA=
 .
.∴AB=OA•tan∠AOB=
 ×
× =1,OB=2,∠BOB′=180°-30°=150°,
=1,OB=2,∠BOB′=180°-30°=150°,∴S△OAB=
 AB•OA=
AB•OA= ×1×
×1× =
= ,
,S扇形BOB′=
 =
= π,
π,则图中阴影部分的面积为
 .
.故答案是:
 .
.点评:本题考查了扇形的面积公式,理解图中阴影部分的面积为:S扇形BOB′-S△OAB是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
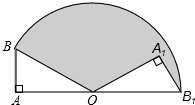 (2012•百色)如图,Rt△OA1B1是由Rt△OAB绕点O顺时针方向旋转得到的,且A、O、B1三点共线.如果∠OAB=90°,∠AOB=30°,OA=
(2012•百色)如图,Rt△OA1B1是由Rt△OAB绕点O顺时针方向旋转得到的,且A、O、B1三点共线.如果∠OAB=90°,∠AOB=30°,OA=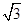 .则图中阴影部分的面积为 .
.则图中阴影部分的面积为 .
 .则图中阴影部分的面积为 .
.则图中阴影部分的面积为 .
 .则图中阴影部分的面积为 .(结果保留π)
.则图中阴影部分的面积为 .(结果保留π)