Question

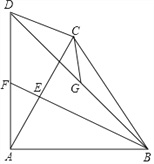
【题目】如图,在四边形ABCD中,,.连接AC、BD,.过点B作,分别交AC、AD于点E、F.点G为BD中点,连接CG.

(1)求证:

(2)根据题中所给条件,猜想:CE与CG的数量关系,并请说明理由.

Answer 1

【答案】（1）证明见解析；（2）

【解析】试题分析：（1）根据AB⊥AD，BE⊥AC，可推导得出∠ABE=∠DAC，再根据∠DCA=∠AEB=90°，AB=AD，即可得△ABE≌△DAC；

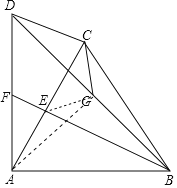
(2)结论:CE=CG，连接AG、EG，证明△CAG≌△EBG，从而得到CG=EG，∠ACG=∠BEG，

继而可得∠ACG=∠CEG=∠GEB，再根据BE⊥AC，从而得∠ACG=∠CEG=∠GEB=45°，得到∠CGE=90°，得到CE=CG.

试题解析：（1）∵AB⊥AD，∴∠BAE+∠DAC=90°，

又∵BE⊥AC，∴∠BAE+∠ABE=90°，

∴∠ABE=∠DAC，

∵AC⊥DC，∴∠DCA=∠AEB=90°，

又∵AB=AD，∴△ABE≌△DAC；

(2)结论:CE=CG，理由如下：

连接AG、EG，

由（1）知BE=AC，∠DAC=∠ABE，

∵∠BAD=90°，AB=AD，G为BD的中点，∴AG=BG，∠DAG=∠BAG=∠ABD=45°，

∵∠DAC=∠ABE，∴∠CAG=∠EBG，

又∵BE=AC，AG=BG，∴△CAG≌△EBG，

∴CG=EG，∠ACG=∠BEG，

∴∠ACG=∠CEG，∴∠ACG=∠CEG=∠GEB，

又∵BE⊥AC，∴∠ACG=∠CEG=∠GEB=45°，

∴∠CGE=90°，∴CE=CG.