Question

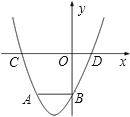
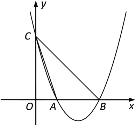
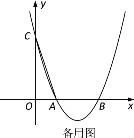
【题目】如图，抛物线交x轴于点和点B，交y轴于点．

（1）求抛物线的解析式；

（2）在抛物线上找出点P，使，求点P的坐标；

（3）将直线AC沿x轴的正方向平移，平移后的直线交y轴于点M，交抛物线于点N．当四边形ACMN为等腰梯形时，求点M、N的坐标．

Answer 1

【答案】（1）；（2）；（3）存在M（0，）、N（，－）使四边形ACMN为等腰梯形.

【解析】

（1）根据抛物线交x轴于点和点B，交y轴于点．用待定系数法直接求出即可；
（2）过P作，垂足为H，PO＝OC，，则CH＝OH 令，解方程即可求出点P的横坐标，即可求解.
（3）连接NA并延长交OC于G，根据等腰梯形的性质得到GA＝GC，设GA＝x，则GC＝x，OG＝3－x在Rt△OGA中，根据勾股定理OA 2＋OG 2＝AG 2，列出方程，解得x＝

∴OG＝3－x＝，求出 直线AG的解析式，联立方程，即可求出点N的坐标.进而求出点M的坐标.

（1）∵抛物线 过点A（1，0）、C（0，3）

∴

解得

∴抛物线的解析式为

（2）过P作，垂足为H

∵PO＝OC，

∴CH＝OH

∴ …

∴

.

（3）连接NA并延长交OC于G

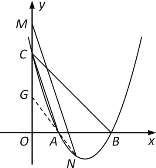
∵四边形ACMN为等腰梯形，且AC∥MN

∴∠ANM＝∠CMN，∠ANM＝∠GAC，∠GCA＝∠CMN

∴∠GAC＝∠GCA，∴GA＝GC

设GA＝x，则GC＝x，OG＝3－x

在Rt△OGA中，OA 2＋OG 2＝AG 2

∴1 2＋( 3－x )2＝x 2，解得x＝

∴OG＝3－x＝ ，∴G（0，）

易得直线AG的解析式为y＝－ x＋

令－ x＋ ＝x 2－4x＋3，解得x1＝1（舍去），x2＝

∴N

∴CM＝AN＝

∴OM＝OC＋CM＝3＋ ＝

∴M（0，）

∴存在M（0，）、N使四边形ACMN为等腰梯形