Question

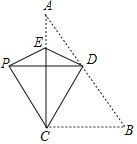
【题目】已知：如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点．

（1）求证：△ABM≌△DCM；

（2）判断四边形MENF是什么特殊四边形，并证明你的结论；

（3）当四边形MENF是正方形时，求AD：AB的值．

Answer 1

【答案】（1）证明见解析（2）菱形（3）2

【解析】

（1）根据矩形的性质得到AB=CD，∠A=∠D=90°，利用SAS定理证明△ABM≌△DCM；

（2）证明ME=MF，根据邻边相等的平行四边形是菱形证明；

（3）证明Rt△BEN≌Rt△CFN，得到∠ENB=∠FNC=45°，∠ABM=45°，得到AB=AM，计算即可．

（1）∵四边形ABCD是矩形，∴AB=CD，∠A=∠D=90°，

又∵M是AD的中点，∴AM=DM．

在△ABM和△DCM中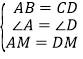，∵，∴△ABM≌△DCM；

（2）四边形MENF是菱形．

∵E，F，N分别是BM，CM，CB的中点，∴NE∥MF，NE=MF，∴四边形MENF是平行四边形．

由（1）得：BM=CM，∴ME=MF，∴四边形MENF是菱形；

（3）∵四边形MENF是正方形，∴EN=NF，NE⊥BM，NF⊥MC，

又∵N是BC的中点，∴BN=NC，

在Rt△BEN和Rt△CFN中，

，∴Rt△BEN≌Rt△CFN，∴∠ENB=∠FNC=45°，∴∠ABM=45°，

∴AB=AM，

又∵M是AD的中点，∴AD：AB=2．