题目内容
如图，C、D、E为线段AB上三点，且AC=
CD，E为BD的中点，DE=
AB=2cm，则CE的长为________cm．
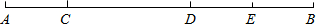
6
分析：先根据DE=AB=2cm求出AB的长，再根据E为BD的中点求出BD的长，进而得出AD的长，再根据AC=CD可求出CD的长，由CE=CD+DE即可得出结论．
解答：∵DE=AB=2cm，
∴AB=2×5=10，
∵E为BD的中点，
∴BD=2DE=2×2=4cm，
∴AD=AB-BD=10-4=6cm，
∵AC=CD，
∴CD=
AD=×6=4m，
∴CE=CD+DE=4+2=6cm．
故答案为；6．
点评：本题考查的是两点间的距离，熟知各线段之间的倍数关系是解答此题的关键．
分析：先根据DE=
AB=2cm求出AB的长，再根据E为BD的中点求出BD的长，进而得出AD的长，再根据AC=CD可求出CD的长，由CE=CD+DE即可得出结论．解答：∵DE=
AB=2cm，∴AB=2×5=10，
∵E为BD的中点，
∴BD=2DE=2×2=4cm，
∴AD=AB-BD=10-4=6cm，
∵AC=
CD，∴CD=
AD=×6=4m，∴CE=CD+DE=4+2=6cm．
故答案为；6．
点评：本题考查的是两点间的距离，熟知各线段之间的倍数关系是解答此题的关键．
练习册系列答案
同步练习强化拓展系列答案
相关题目
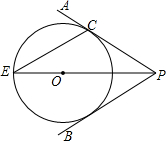如图，点O在∠APB的平分线上，⊙O与PA相切于点C．
如图，DE是△ABC的中位线，FG为梯形BCED的中位线，若BC=8，则FG等于
如图，三角形ABC中，D为BC上的一点，且S△ABD=S△ADC，则AD为（ ）| A、高 | B、角平分线 | C、中线 | D、不能确定 |
（2013•保康县二模）如图，在⊙O中，AB为直径，弦CD⊥直径AB于点M．